Obtener la ecuación de la circunferencia conocida su gráfica

Para lograrlo debemos conocer dos elementos importantes:

- el centro de la circunferencia (C), dado por sus coordenadas

- el radio (r) de la misma circunferencia

Definido esto, tendremos dos posibilidades :

A) Circunferencia con centro (C) en el origen de las coordenadas; expresado como C (0, 0)

B) Y circunferencia con centro (C) fuera del origen de las coordenadas; expresado, por ejemplo, como C (3, 2) .

Circunferencia con centro (C) en el origen de las coordenadas; expresado como C (0, 0)

A continuación analizaremos cuatro casos

Caso 1

Veamos la gráfica siguiente:

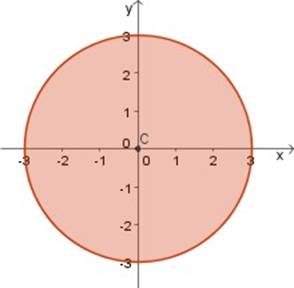
Los datos que nos entrega son:

Centro: C (0, 0) , el centro se ubica en el origen de las coordenadas x e y

radio: r = 3 , lo indica el 3 en cada una de las coordenadas.

Recordar esto:

Cuando el centro (C) de la circunferencia sea (0, 0) se usará la ecuación x ² + y ² = r ² para expresar dicha circunferencia en forma analítica ( Geometría analítica ) . Esta ecuación se conoce como ecuación reducida .

Para la gráfica de nuestro ejemplo, reemplazamos el valor de r en la fórmula x ² + y ² = 3 ²
y nos queda x ² + y ² = 9 como la ecuación reducida de la circunferencia graficada arriba.

Ojo:

Si nos dieran la ecuación x ² + y ² = 9 y nos preguntaran qué representa, razonamos en sentido inverso y diremos que representa una circunferencia, con centro (C) en el origen de las coordenadas (0, 0) y cuyo radio es 3 (3 ² = 9 y la raíz cuadrada de 9 es 3)

Circunferencia con centro (C) en el origen de las coordenadas; expresado como C (0, 0)

Caso 2

Veamos la gráfica siguiente:

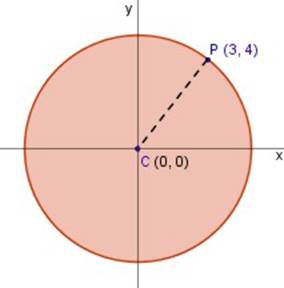
Los datos que nos entrega son:

Centro: C (0, 0) , el centro se ubica en el origen de las coordenadas x e y

radio: r , lo desconocemos, pero tenemos un dato: el punto P (3, 4) ubicado en la circunferencia.

Recordemos de nuevo :

Cuando el centro (C) de la circunferencia sea (0, 0) se usará la ecuación x ² + y ² = r ² para expresar dicha circunferencia en forma analítica. Esta ecuación se conoce como ecuación reducida .

Para la gráfica de nuestro ejemplo, deberíamos colocar el valor de r en la fórmula x ² + y ² = r ² , pero resulta que no lo conocemos.

Entonces, a partir del dato P (3, 4) podemos calcular el valor del trazo que une este punto con el centro C (0, 0) (trazo PC con línea punteada en la figura), el cual corresponde al radio de la circunferencia dada.

¿Cómo calculamos el valor de la distancia (d) entre P y C (el radio de la circunferencia)?

Para calcular la distancia (d) entre dos puntos (encontrar su valor) contamos con la siguiente fórmula:

No olvidemos que esta fórmula es para encontrar o conocer la distancia entre dos puntos ; por lo mismo, debemos saber que en ella

(x ₂ ─ x ₁ ) ² representa al punto 1, y ese punto 1 (P ₁ ) lo haremos corresponder con el punto que pasa por el centro C (0, 0)

(y ₂ ─ y ₁ ) ² representa al punto 2, y ese punto 2 (P ₂ ) lo haremos corresponder con el punto que pasa por P (3, 4).

Es muy importante conocer o designar este orden ya que

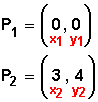
ecuacion_circunferencia006

Establecido este orden o equivalencia, podemos sustituir los valores en la fórmula anterior para conocer la distancia (d) entre los dos puntos que nos interesan, la cual será nuestro radio:

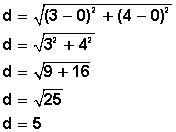
ecuacion_circunferencia007

El 5 nos indica la distancia entre los dos puntos, el centro de la circunferencia y uno de sus puntos, lo cual corresponde al radio .

Recapitulemos:

Para expresar u obtener la ecuación de una circunferencia cuyo centro está en el origen, necesitamos conocer el centro, ya sabemos que es C (0, 0), y conocer el radio, que ahora sabemos que es 5.

¿Se acuerdan cuál es la fórnula?

Esta: x ² + y ² = r ²

Reemplazamos en ella el valor del radio

x ² + y ² = 5 ² y nos queda

x ² + y ² = 25 como la ecuación reducida de la circunferencia graficada arriba (en la cual nos indicaron un centro y un punto en ella).

Ojo:

Si nos dieran la ecuación x ² + y ² = 25 y nos preguntaran qué representa, razonamos en sentido inverso y diremos que representa una circunferencia, con centro (C) en el origen de las coordenadas (0, 0) y cuyo radio es 5 (5 ² = 25 y la raíz cuadrada de 25 es 5).

Circunferencia con centro (C) en el origen de las coordenadas; expresado como C (0, 0)

Caso 3

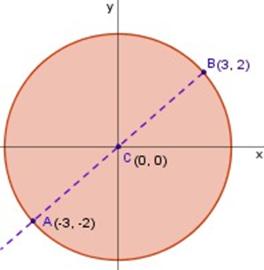
Tenemos la gráfica de una circunferencia cuyo centro (C) es el origen de las coordenadas (0, 0), y nos dan dos puntos opuestos en la circunferencia, , A (-3, -2) y B (3, 2), los cuales unidos corresponden al diámetro de la misma.

Recordemos de nuevo :

Para la gráfica de nuestro ejemplo, deberíamos colocar el valor de r en la fórmula x ² + y ² = r ² , pero resulta que no lo conocemos.

Pero tenemos identificados dos puntos opuestos en la circunferencia, los cuales unidos entre sí (la línea punteada entre A y B en la gráfica) representan al diámetro de la misma. Entonces, a partir de esos puntos, A (-3, -2) y B (3, 2), podemos calcular el valor del trazo que los une (trazo AB con línea punteada en la figura), el cual corresponde al diámetro de la circunferencia dada.

¿Cómo calculamos el valor de la distancia (d) entre A y B (el diámetro de la circunferencia)?

Para calcular la distancia (d) entre dos puntos (encontrar su valor) contamos con la siguiente fórmula:

No olvidemos que esta fórmula es para encontrar o conocer la distancia entre dos puntos; por lo mismo, debemos saber que en ella

(x ₂ ─ x ₁ ) ² representa al punto 1, y ese punto 1 (P ₁ ) lo haremos corresponder con el punto A (-3, -2)

(y ₂ ─ y ₁ ) ² representa al punto 2, y ese punto 2 (P ₂ ) lo haremos corresponder con el punto B (3, 2).

Es muy importante conocer o designar este orden ya que

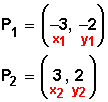
ecuacion_circunferencia009

Establecido este orden o equivalencia, podemos sustituir los valores en la fórmula anterior para conocer la distancia (d) entre los dos puntos que nos interesan, la cual será nuestro diámetro

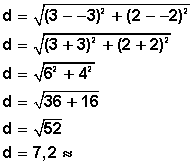
ecuacion_circunferencia010

El 7,2 (valor aproximado) nos indica la distancia entre los dos puntos, A y B, la cual corresponde al diámetro de la circunferencia.
Para conocer el valor del radio, simplemente dividimos por 2 dicho diámetro, y nos queda r = 3,6 ≈

Conocido el radio lo reemplazaremos en la ecuación de la circunferencia cuyo centro está en el origen de las coordenadas, que es:

x ² + y ² = r ²

la cual nos queda

x ² + y ² = (3,6) ² .

x ² + y ² = 13 ≈ como la ecuación reducida de la circunferencia graficada arriba (en la cual nos indicaron un centro y dos puntos opuestos en ella).

Esta ecuación también podía obtenerse haciendo el cálculo para la distancia entre uno de los puntos dados y el centro, como se vio en el caso 2

Ojo:

Si nos dieran la ecuación x ² + y ² = 13 y nos preguntaran qué representa, razonamos en sentido inverso y diremos que representa una circunferencia, con centro (C) en el origen de las coordenadas (0, 0) y cuyo radio es 3,6 (3,6) ² = 13 y la raíz cuadrada de 13 es 3,6 ≈).

Circunferencia con centro (C) en el origen de las coordenadas; expresado como C (0, 0)

Caso 4

Tenemos la gráfica de una circunferencia con centro (C) en el origen de las coordenadas (0, 0), no hay otro dato sobre coordenadas, pero se me indica que tiene un área de 10 u ² (diez unidades cuadráticas).

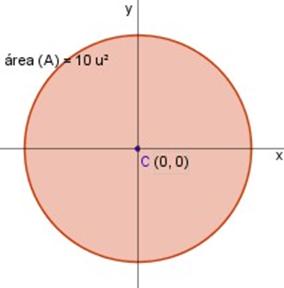
Recordemos de nuevo :

Para la gráfica de nuestro ejemplo, deberíamos colocar el valor de r en la fórmula x ² + y ² = r ² , pero resulta que no lo conocemos.

Pero conocemos el área de la circunferencia (10 u ² ) y a partir de este dato podemos calcular el radio de la misma.

¿Cómo calculamos el radio de la circunferencia si conocemos su área ?

Repasemos el cálculo del área (A) de una circunferencia :

A = π • r ²

A = 10 (dato conocido),

entonces 10 = π • r ² y

, este dato podría ser suficiente para reemplazar el valor de r ² en la fórmula, pero podemos avanzar un poco y hacemos

Volvamos a nuestra fórmula inicial

x ² + y ² = r ²

Como ahora conocemos el radio:

x ² + y ² = (1,78) ²

x ² + y ² = 3,18 ≈

También pudimos hacer

Ojo:

Si nos dieran la ecuación x ² + y ² = 3,18 ≈ y nos preguntaran qué representa, razonamos en sentido inverso y diremos que representa una circunferencia, con centro (C) en el origen de las coordenadas (0, 0) y cuyo radio es 1,78 (1,78) ² = 3,18 y la raíz cuadrada de 3,18 es 1,78 ≈).

Ir a:

Obtener la Ecuación de la circunferencia con centro (C) fuera del origen de las coordenadas