Pendiente de la recta |
Antes de referirnos a la orientación de una pendiente de la recta (si es positiva o negativa ) hagamos una recapitulación:
Veamos un ejemplo.
Si tenemos
y = 3x − 4
esto es igual a,
3x − y − 4 = 0
(ecuación de la recta)
Ahora lo que sigue es sacar la pendiente, pero ¿Cómo se obtiene la pendiente si solo tenemos la fórmula?
Pues hay dos maneras de hacerlo:
directa
e
indirecta
:
Indirecta:
Obtenemos dos puntos ( x e y ) a partir de dos valores dados a x (por ejemplo, x = 1 y x = 2 ), y los ponemos en la ecuación de la recta:
3x − y − 4 = 0 si (x = 1)
3(1) − y − 4 = 0
3 − y − 4 = 0
− y − 1 = 0
y + 1 = 0
y = − 1
P
1
(1, −1) = (x
1
, y
1
)
3x − y − 4 = 0
si (x = 2)
3(2) − y − 4 = 0
6 − y − 4 = 0
− y + 2 = 0
y = 2
P
2
(2, 2) = (x
2
, y
2
)
Ahora sustituimos en la fórmula de la pendiente:
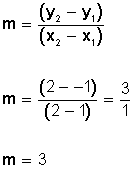
(esta es la pendiente)
Directa:
Basándonos en los valores de la recta podemos conseguir la pendiente:
3x − y − 4 = 0
Ax − By − C = 0
A = cantidad de
x
B = cantidad de y
C = Número cualquiera
Ahora solo sustituimos en la fórmula de la pendiente
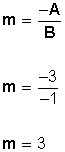
(esta es la pendiente)
Grado de inclinación
Dada una recta, gráficamente su pendiente nos da su grado de inclinación
Pendiente positiva
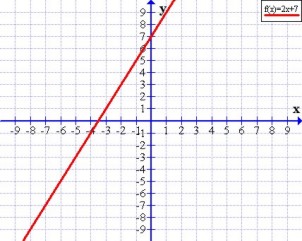
Cuando la recta es creciente (al aumentar los valores de x aumentan los de y), su pendiente es positiva, en la expresión analítica m > 0
Pendiente negativa
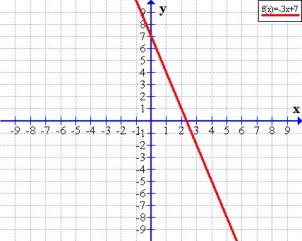
Cuando la recta es decreciente (al aumentar los valores de x disminuyen los de y), su pendiente es negativa, en la expresión analítica m < 0
Pendiente nula o cero
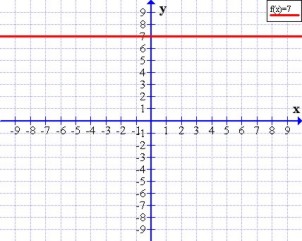
Cuando la recta es constante se dice que tiene pendiente nula, en la expresión analítica m = 0
Visualmente, también podemos definir si la pendiente es positiva o negativa:
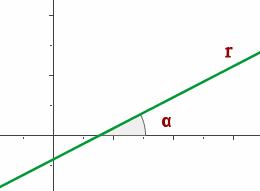
Si el ángulo que forma la recta con la parte positiva del eje OX es agudo , la pendiente es positiva y crece al crecer el ángulo.
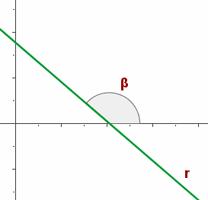
Si el ángulo que forma la recta con la parte positiva del eje OX es obtuso , la pendiente es negativa y decrece al crecer el ángulo.
Con los ejemplos discutidos podemos observar la interpretación geométrica de la pendiente de una recta:
| Pendiente |
Tipo de recta |
|
positiva |
recta ascendente |
|
negativa |
recta descendente |
|
cero |
recta horizontal |
|
no definida |
recta vertical |
Ver: PSU: Matemática,
Volver a: Ecuación de la recta
Ver en Internet:
http://www.cidse.itcr.ac.cr/revistamate/Herramientas/Recta/Recta.html
http://www.uprh.edu/~eudez/web%20mecu/docsPDFdeMECU/leccion8.PDF

