Teoremas de Euclides |
De Euclides (330 a.C al 227 a.C) se sabe muy poco, con certeza, acerca de sus vida. Su gran reputación se debe sin duda a su obra titulada Los Elementos Geométricos , conocida simplemente por Los Elementos .
Además de estas y otras obras, Euclides escribió Los Datos que trata de la resolución de problemas, dándose elementos de la figura y determinándose otros. Los Porismos es una de sus obras perdidas; se cree que trataba de los Lugares Geométricos y de proposiciones sobre transversales. Muchos piensan que esta ha sido la mejor obra de Euclides.
A continuación se presentan dos Teoremas de Euclides, uno referido a un cateto (en un triángulo rectángulo) y otro referido a la altura.
Teorema de Euclides referido a un cateto
“En un triángulo rectángulo la medida de cada cateto es media proporcional geométrica entre las medidas de la hipotenusa y su proyección sobre ella.”
Demostración:
|
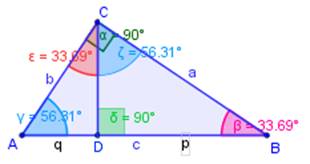
Si se tiene un triángulo ABC cualquiera, rectángulo en C , y se proyectan los catetos sobre la hipotenusa, se tiene la figura de arriba:
donde
DB = p (proyección del cateto a (CB) sobre la hipotenusa)
AD = q (proyección del cateto b (AC) sobre la hipotenusa)
c = p + q
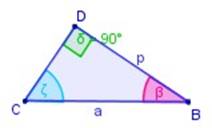
Por semejanza (~) de triángulos, el ΔACB ~ ΔCDB (son semejantes)
|
Luego;
![]()
Que es lo mismo que:
![]()
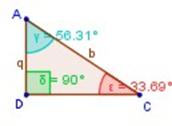
De forma análoga se tiene que ΔACB ~ ΔADC (figura de abajo) ,
|
|
|
entonces
![]()
Que es lo mismo que:
![]()
Ver: PSU: Geometría; Pregunta 09_2005
Vistas las fórmulas a las que arribamos utilizando la media proporcional geométrica, podemos enunciar el primer Teorema de Euclides también de la siguiente forma:
“En un triangulo rectángulo, el cuadrado de un cateto es igual al producto de la hipotenusa por la proyección del mismo cateto sobre la hipotenusa”.
Por lo tanto,
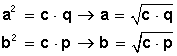
Ejemplos:
|
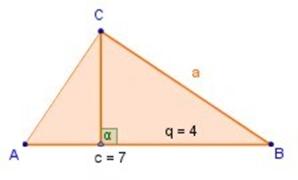
1) En la figura de arriba, determinar a ,
si c = 7 y q = 4
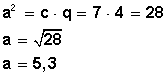
2) En la figura de abajo,
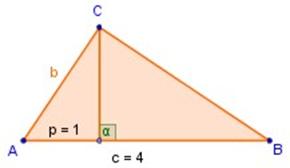
|
determinar b
si c = 4 y p = 1
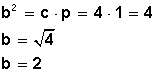
Teorema de Euclides relativo a la altura
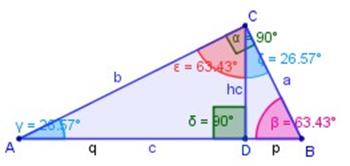
“En un triángulo rectángulo la altura correspondiente a la hipotenusa es media proporcional geométrica entre los segmentos que dicha altura determina en ella.”
|
Se sabe que ΔADC ~ ΔCDB (semejantes, en la figura superior); por lo tanto, sus lados homólogos (correspondientes) son proporcionales.
Sea hc (CD) la altura de la hipotenusa (AB = c)
Entonces:
![]()
Reemplazando:
![]()
Llegamos a:
![]()
A partir de esta última fórmula, y tal como en el caso del primer teorema de Euclides, este segundo teorema también se puede expresar de la siguiente manera:
“En un triangulo rectángulo, el cuadrado de la altura de la hipotenusa (hc) es equivalente al producto de las proyecciones de los catetos en la hipotenusa”.
Por lo tanto, si h 2 = p • q
entonces
![]()
Ejemplos:
|
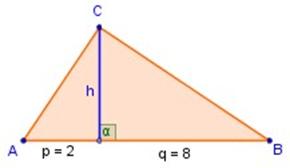
1) En la figura superior, determinar h ,
si p = 2 y q = 8

|
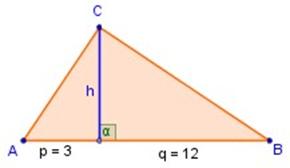
2) En la figura superior, determinar h ,
si p = 3 y q = 12
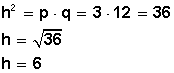
![]()