Volumen |
El volumen es el espacio que ocupan los cuerpos.
Los cuerpos geométricos existen en el espacio y son por lo tanto objetos que tienen tres dimensiones (ancho, alto y largo) limitados por una o más superficies. Si todas las superficies son planas y de contorno poligonal, el cuerpo es un poliedro. Si el cuerpo no está limitado por polígonos, sino por superficies curvadas recibe el nombre de cuerpos redondos.
La fórmula para calcular el volumen de un cuerpo depende de su forma.
Para medir el volumen de un cuerpo se utilizan unidades cúbicas, que son: milímetro cúbico, centímetro cúbico, decímetro cúbico y metro cúbico
|
mm
3
, cm
3
, dm
3
, m
3
|
Para determinar el volumen de los cuerpos geométricos se debe tener en cuenta lo siguiente:
1.- El volumen de un cubo es igual al cubo de uno de sus lados, esto se expresa como:
|
V = l
3
|
2.- El volumen de un prisma es igual al producto del área de la base por la altura, esto se expresa como:
|
V = Bh
|
3.- El volumen de un cilindro es igual al producto de p por el cuadrado del radio por la altura, esto se expresa como:
|
V = Π r 2 h |
4.- El volumen de una pirámide es igual a la tercera parte del producto del área de la base por la altura, lo cual se expresa como:
|
V = B h ÷ (dividido o partido por) 3 |
5.- El volumen del cono es igual a la tercera parte del producto de pi por el cuadrado del radio por la altura, lo cual se expresa como:
|
Π r 2 h ÷ (dividido o partido por) 3 |
Con base en lo anterior se pueden resolver problemas que impliquen determinar el volumen de algún cuerpo geométrico.
1. La altura de
un prisma pentagonal es de
Los datos con los que se cuenta son:
longitud de los lados =
longitud del apotema (a) =
altura del prisma =
Primero se procede a determinar el área de la base (B):
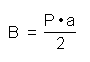
|
El perímetro (P) se halla multiplicando la longitud de uno de los lados por cinco, ya que se trata de un pentágono.
Sustituyendo valores se tiene:
|
|
Una vez que se tiene el área de la base, se determina el volumen de este prisma con la fórmula V = Bh
Sustituyendo valores se tiene:
V = 440 cm² (
Esto indica que el volumen de este prisma pentagonal es de 8.800 cm³.
2. Si la base de una pirámide rectangular tiene por dimensiones 10 dm de largo y 8 dm de ancho, y la altura de la pirámide es de 15 dm, ¿cuál es su volumen?
Los datos con que se cuenta son:
largo de la base = 10 dm
ancho de la base = 8 dm
altura de la pirámide = 15 dm
Se determina el área de la base (B):
B = largo x ancho
Sustituyendo valores:
B = 10 dm (8 dm) = 80 dm²
Se aplica la fórmula para calcular el volumen de una pirámide:
![]()
Sustituyendo valores:
V = 80 dm² (15 dm) = 1.200 dm³
El volumen de esta pirámide rectangular es de 1.200 dm³; con base en lo anterior se concluye que:
|
El volumen de los prismas y las pirámides se determina aplicando fórmulas, en las cuales se relaciona su longitud, altura y anchura, mientras que en el cilindro y el cono se relacionan el radio y la altura. |
Volumen de una esfera
En el caso de una esfera (cuerpo limitado por una superficie esférica, es decir, es la superficie que se crea cuando una semicircunferencia gira en torno a su diámetro) el volumen se calcula usando la siguiente fórmula:
Volumen esfera : 4 / 3 · p · R 3
p = 3,1415...
R = Radio
Ejemplo: Si el radio de una circunferencia
es de
V = 4 / 3 · 3.1415.. · ( 4 ) 3
V = 4 / 3 · 3,1415..· 64
V = 804,24772 .
3
V = 268,08 cm 3
El diámetro corresponde a la medida de dos radios y es el segmento de mayor longitud que gira dentro de la circunferencia.
Ver: Cuadro de fórmulas para áreas y volúmenes

