Ángulos en la circunferencia |
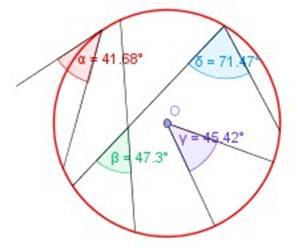
Dibujando líneas que estén dentro de una circunferencia o que tengan relación con ella podemos definir distintos tipos de ángulos , como se aprecia en la figura abajo:
|
Donde:
δ (delta) = ángulo inscrito (71,47º), con el vértice sobre la circunferencia y con lados que son cuerdas de la misma.
α (alfa) = ángulo semiinscrito (41,68º) , cuyo vértice está en la circunferencia y tiene un lado que es tangente en dicho vértice y el otro que es una cuerda.
γ (gama) = ángulo central o del centro (45,42º), con el vértice en el centro de la circunferencia y con sus lados coincidentes con radios .
β (beta) = ángulo interior (47,3º), con sus lados que son cuerdas de la circunferencia y con el vértice situado en el interior de la misma.
A continuación veremos algunas características de estos ángulos y analizaremos ciertas relaciones entre ellos.
Ángulo inscrito en la circunferencia
El ángulo inscrito en una circunferencia es aquel que tiene su vértice sobre la circunferencia y cuyos lados son dos cuerdas de la misma (si las cuerdas se prolongan, diremos que son dos rectas secantes ).
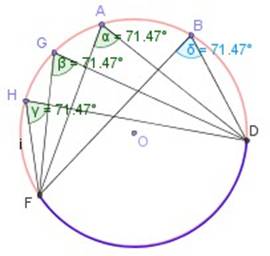
En la figura abajo, vemos varios ángulos inscritos que abarcan o subtienden el arco FD .
|
Todos miden lo mismo (71,47º), por ello, podemos afirmar que “los ángulos inscritos que abarcan el mismo arco son iguales” .
En nuestro ejemplo, son iguales los ángulos de vértices B, A, G, H.
También debemos recordar que un ángulo inscrito vale la mitad del arco que abarca .
El ángulo se expresa en grados. El valor de un arco se expresa en grados y
coincide con el valor del ángulo del centro correspondiente.
Cuando el arco comprendido entre los radios tiene la longitud de éstos, el valor del ángulo central es un radián , una circunferencia tiene pues 2π radianes.
Ángulo central o del centro en la circunferencia
El
ángulo central o del centro
es el que tiene el vértice en el centro de la circunferencia, siendo sus lados dos radios.
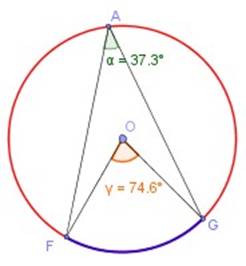
En la figura siguiente, vemos que el ángulo del centro dibujado, con vértice en O, abarca o subtiende el
arco FG
.
|
Al respecto, debemos reiterar que “El ángulo del centro mide lo mismo que el arco que abarca” .
En la misma figura de la derecha se dibujó un ángulo inscrito (α = 37,3º) que subtiende o abarca el mismo arco que el ángulo del centro (γ = 74,6º) ; en dicha situación (y los valores indicados lo confirman), “ Cuando un ángulo inscrito y un ángulo del centro de una circunferencia abarcan el mismo arco, el ángulo inscrito vale la mitad que el del centro”.
Ver: PSU: Geometría;
|
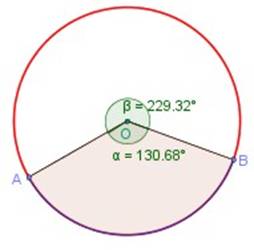
Es importante notar que dos puntos, A y B, sobre una circunferencia determinan dos arcos y, por tanto, dos ángulos centrales: uno cóncavo (α = 130,68º) y uno convexo (β = 229,32º) , o los dos iguales, que sumarán 360º .
|
|
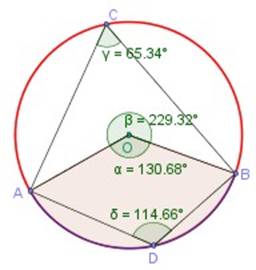
Los ángulos inscritos ( γ = 65,34º y δ = 114,66 en la figura abajo) que subtienden los mismos arcos que subtienden los ángulos del centro mencionados, serán suplementarios, pues sumarán siempre 180º .
|
Ángulo semiinscrito en la circunferencia
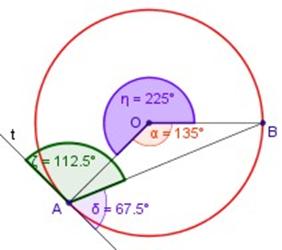
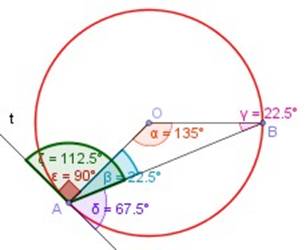
El ángulo semiinscrito tiene el vértice A en la circunferencia, siendo sus lados la recta t tangente en A y la cuerda AB (figura a la izquierda).
La tangente, que es perpendicular al radio, es lado de dos ángulos semiinscritos y cada uno subtiende un arco diferente.
Un ángulo
semiiscrito
(en la figura es
δ = 67,5º
) vale la mitad que el ángulo del centro (
α = 135º
) que abarca el arco
AB
.
|
Nótese que en la figura están dados los valores de los ángulos y es fácil comprobar lo antes dicho, pero para comprobarlo de modo general, sin saber los valores, calculamos el valor del ángulo central así:
,
por pertenecer al triángulo isósceles ABC (recordar que los ángulos interiores de cualquier triángulo suman 180º, y que el triángulo isósceles tiene dos ángulos iguales).
Entonces, calculamos el valor del ángulo δ semiinscrito:
|
El razonamiento es el mismo cuando el ángulo semiiscrito (ζ (zeta) = 112,5º) abarca el otro arco definido por AB .
|
Ángulo interior en la circunferencia
|
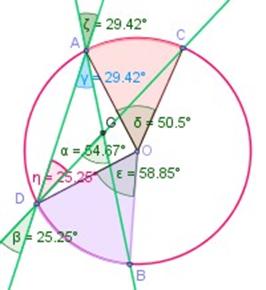
El ángulo interior α tiene el vértice en un punto interior de la circunferencia, en el círculo . Sus lados son dos rectas secantes.
El ángulo interior
, siendo
δ
y
ε
los ángulos centrales de los arcos (AC y DB) definidos por las rectas secantes.
Vamos a comprobarlo:
Consideramos el triángulo escaleno AGD :
el ángulo
, pues es el ángulo inscrito que abarca el arco
AC
;
el ángulo
, pues es el ángulo inscrito que abarca el arco
DB
;
entonces el ángulo
,
por lo tanto,
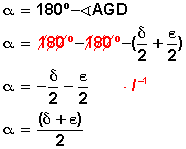
Ángulos exteriores a la circunferencia
|
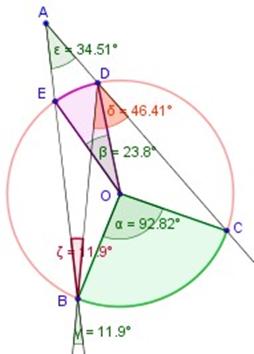
El ángulo exterior ε tiene el vértice (A) en un punto exterior a la circunferencia. Sus lados son dos rectas secantes (AB y AC) .
El ángulo exterior
, siendo
α y β
los ángulos centrales de los dos arcos definidos por las dos rectas secantes.
Vamos a comprobarlo:
Consideramos el triángulo escaleno ADB:
el ángulo
, pues es el ángulo inscrito que abarca el
arco ED
;
el ángulo
, pues es el ángulo inscrito que abarca el
arco BC
;
el ángulo
, suplementario de
CDB
;
por lo tanto, el ángulo
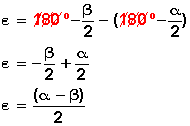
Hay otros dos casos de ángulos exteriores, según sus lados sean secantes o tangentes a la circunferencia:
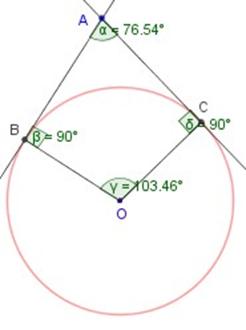
El ángulo exterior circunscrito α (figura de la izquierda) tiene los dos lados tangentes a la circunferencia; α = 180º — γ , siendo γ el ángulo central BOC definido por las tangentes.
Vamos a comprobarlo:
|
El cuadrilátero ABOC cumple, como tal, que la suma de sus ángulos interiores es 360º.
Siendo dos de sus ángulos rectos (β y δ) , resulta que 180º = α + γ ,
luego α = 180º — γ .
El
ángulo exterior circunscrito γ
tiene un lado secante y otro tangente a la circunferencia (figura a la derecha).
El
ángulo exterior
, siendo
α y β
los ángulos centrales de los arcos definidos por sus lados.
Vamos a comprobarlo:
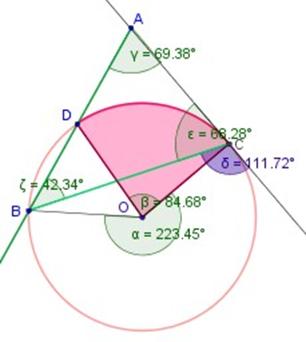
Consideramos el triángulo escaleno ABC :
|
el ángulo
, pues es el
ángulo inscrito
que abarca el arco
CD
;
el ángulo
, pues es el ángulo suplementario de
δ
, ángulo semiinscrito que abarca el arco BC;
el ángulo
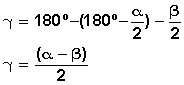
Fuente Internet:
http://www.educared.org/wikiEducared/%C3%81ngulos_en_las_circunferencias.html
Los contenidos de Wikillerato están disponibles bajo una licencia de Creative Commons . Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.
Ver:
http://filemon.upct.es/~pepemar/angulo/home.htm
http://www.aulafacil.com/matematicas-basicas/geometria/curso/Lecc-42.htm