División de expresiones algebraicas

Repaso de conceptos

Una expresión algebraica es aquella en la que se utilizan letras, números y signos de operaciones.

Por ejemplo,

Suma de cuadrados: a ² + b ²

Triple de un número menos doble de otro: 3x - 2y

Suma de varias potencias de un número: a ⁴ + a ³ + a ² + a

Las expresiones algebraicas se clasifican según su número de términos.

Clases de expresiones algebraicas:

1. Si una expresión algebraica está formada por un solo término se llama monomio.

Ejemplo: 3ax ²

2. Si la expresión algebraica tiene varios términos se llama polinomio .

3. Cuando un polinomio esta formado por dos términos se llama binomio .

Ejemplo: 2x ² + 3xy

4. Cuando un polinomio esta formado por tres términos se llama trinomio .

Ejemplo: 5x ² + 4y ⁵ – 6x ² y

División de monomios

Para dividir monomios se resta los exponentes de las potencias de misma base siguiendo la ley de los exponentes

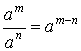
Ejemplo:

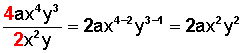
División de un polinomio por un monomio

Para dividir un polinomio entre un monomio basta con dividir cada uno de los términos del dividendo entre el término del divisor.

Ejemplo:

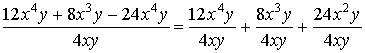
restando los exponentes de las potencias de la misma base se obtiene el resultado:

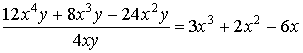
División de polinomios entre polinomios

La división algebraica se realiza de manera semejante a la numérica;

Si se tiene la división

1. Se ordenan de manera decreciente los términos de los polinomios, quedando la división:

2. Se obtiene el primer término del cociente dividiendo el primer término del dividendo (–2x ² ) por el primer término del divisor (x):

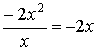
3. Se anota como cociente (-2x) y se multiplica por el divisor (x+4), se anotan los productos debajo del dividendo y se realiza la sustracción.

4. se vuelve a dividir el primer término que quedó en el dividendo (3x) por el primero del divisor (x) y se repite el proceso anterior.

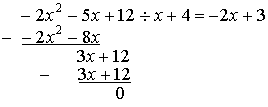
Se ha obtenido cociente –2x + 3 y resto 0