Ecuación exponencial

Una ecuación exponencial es aquella ecuación que incluye alguna potencia en cualquiera de sus términos y en que la incógnita aparece en el exponente.

Para resolver una ecuación exponencial debemos tener en cuenta que:

(a debe ser mayor que cero y distinto de 1)

y que si

(si la base a es igual a la base a , entonces los exponentes serán iguales entre sí )

También debemos recordar las propiedades de las potencias , las que se describen a continuación:

a ⁰ = 1

Toda potencia elevada a cero es igual a 1

a ¹ = a

Toda potencia elevada a 1 es igual a la base

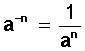
Ecuacion_exponencial003

Toda potencia con exponente negativo es igual al inverso de su base, ahora con exponente positivo en el denominador.

Toda potencia elevada a un exponente fraccionario es igual a una raíz de la base elevada al numerador de la fracción , y el índice de la raíz corresponde al denominador de la fracción.

a ^m • a ⁿ = a ^m+n

Para multiplicar dos potencias de igual base y distintos exponentes , se conserva la base y esta se eleva a la suma de los exponentes.

a ^m : a ⁿ = a ^{m − n}

Para dividir dos potencias de igual base y distintos exponentes , se conserva la base y esta se eleva a la resta de dichos exponentes.

(a ^m ) ⁿ = a ^{m · n}

Para elevar una potencia a potencia , se conserva la base y se multiplican los exponentes.

a ⁿ • b ⁿ = (a · b) ⁿ

Para multiplicar potencias de distinta base, pero con igual exponente , se multiplican las bases y se conserva el exponente único o común.

a ⁿ : b ⁿ = (a : b) ⁿ

Para dividir potencias de distinta base, pero con igual exponente , se dividen las bases y se conserva el exponente único o común.

Nota importante

Debemos tener presente que no existe ninguna fórmula general que indique cómo resolver cualquier ecuación exponencial. Sólo la práctica ayuda a decidir, en cada caso, qué camino tomar.

De todos modos, para resolver una ecuación exponencial hay que realizar algunas acciones previas que son imprescindibles:

Primero:

Si los dos miembros de la igualdad tienen distinta base, debemos reducirlos a la misma base.

Ejemplo:

Segundo:

Una vez que tenemos la misma base en los dos miembros, igualamos los exponentes y resolvemos la ecuación.

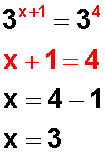
Ecuacion_exponencial006

Y aquí es donde empiezan las dificultades, ya que si no dominamos las propiedades de las potencias se hará muy difícil resolver este tipo de ecuaciones.

El uso de los logaritmos , como veremos luego en Ecuaciones logarítmicas , facilita en muchas ocasiones la resolución de estas ecuaciones.

Veamos y tratemos de resolver un problema con ecuación exponencial

Sea que tengamos la ecuación exponencial

Vemos que todas las bases son distintas; por lo tanto, trataremos de igualar dichas bases para que nos quede:

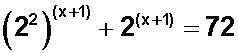
Ecuacion_exponencial008

Ahora tenemos que el primer término es una potencia elevada a potencia , y deberíamos expresar la ecuación como

Pero, por conveniencia, invertimos los exponentes del primer término, y la expresamos así:

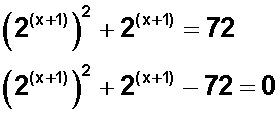
Ecuacion_exponencial010

Y vemos que esta ecuación exponencial es una ecuación de segundo grado .

Para resolverla, es necesario el uso de incógnitas auxiliares . Así el problema se simplifica y es fácil comprobarlo.

La incógnita auxiliar para esta ecuación exponencial es:

2 ^{(x + 1)} = U

Hecho esto, reemplazamos los valores con la incógnita auxiliar, para luego resolver:

U ² + U − 72 = 0

Esta ecuación podría resolverse mediante la fórmula general para resolver ecuaciones de segundo grado , pero como corresponde al caso de factorización de un trinomio perfecto es conveniente por su rapidez utilizar dicha factorización.

Se debe recordar que para hacerla hay que buscar dos números que multiplicados den –72 y que sumados , al mismo tiempo, den 1 (positivo) . Estos números son: 9 y –8 .

Factorizando queda: