Suma (adición) de fracciones |
En la resolución de problemas con fracciones (o números racionales Q) es necesario tener en cuenta las fracciones decimales y los números mixtos .
Las fracciones decimales son aquellas que tienen denominador 10, 100, 1.000, o cualquier otro múltiplo de 10.
Siempre que se convierte un número decimal en fracción común se obtiene una fracción decimal.
Ejemplos:
a) Al convertir 0,8 (ocho décimas) en fracción común, se obtiene
b) Al convertir 0,29 (veintinueve centésimas) en fracción común, se obtiene
c) Al convertir o,135 (ciento treinta y cinco milésimas) en fracción común, se obtiene
Los números mixtos son aquellos que están formados por un número entero y una fracción común; para sumarlos o restarlos se convierten en fracciones impropias (aquellas cuyo numerador es mayor que el denominador) y después se efectúa la operación.
Ejemplos:
Ejemplo a)
Para convertir un número mixto en fracción impropia se multiplica el entero por el denominador y al producto se le suma el numerador; el denominador se conserva igual.
Entonces
Ahora que tenemos la fracción impropia se realiza la adición; para ello se busca el mínimo común múltiplo (m.c.m.) de los denominadores (debe buscarse siempre el m.c.m. cuando los denominadores son distintos), después se transforman las fracciones a sus equivalentes (que tengan el mismo denominador).
m.c.m. (3, 4) = 12
Se puede operar así:
O bien así:
y
Sumamos
Este resultado se puede convertir en número mixto, haciendo una división.
Ejemplo b)
Se
convierte el número mixto en fracción impropia:
Se convierte el número decimal en fracción común:
0,5 =
Para efectuar la adición se busca el mínimo común múltiple de los denominadores, luego se transforman las fracciones a los equivalentes que tengan el mismo denominador.
m.c.m. (3, 10) = 30
Se puede operar así:
O así:
y
Este resultado lo podemos convertir en número mixto haciendo la división:
Donde 8 (el entero del número mixto) es el cuociente (el resultado de la división), 5 es el resto de la misma y 30 es el denomnador que se conserva igual.
Ahora que hemos visto cómo hacer adiciones con números mixtos y fracciones decimales, resolvamos algunos problemas.
Ejemplo 1:
Al realizar una encuesta entre 100 personas, se les preguntó el tipo de música que preferían escuchar: 60 escogieron la tropical, 25 la romántica y 15 se decidieron por la popular. ¿Cuántas de ellas prefieren escuchar música popular o romántica?
Veamos los datos:
Romántica: 25 de cada 100 , que se expresa como
Popular: 15 de cada 100, que se expresa como
Para obtener la cantidad de personas que prefiere escuchar estos tipos de música, se suman ambas cantidades
Esto indica que 40 de cada 100 personas escuchan música romántica o popular.
Ejemplo 2:
Al preparar una comida, se compraron 3 ½ Kg. de carne de pollo y 2 ¼ Kg. de carne de vacuno; se desea saber cuál es el total de kilogramos de carne que se compró para la comida.
Se convierten los números mixtos en fracciones:
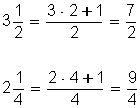
Se busca el mínimo común múltiplo de los denominadores; luego estas fracciones se convierten en fracciones equivalentes con el mismo denominador.
m.c.mm (2, 4) = 4
Sumamos
Este resultado se puede convertir en número mixto:
Esto
indica que en total se compraron
kg de
carne.
Ejemplo 3:
David compró dos metros de plástico para forrar sus cuadernos y libros,
ocupó para ello
de
metro y su hermano, para forrar un cuaderno, usó 0,40m. ¿Cuánto plástico
utilizaron para forrar los libros y los cuadernos?
Se
convierten
y
0,40 en fracciones comunes:
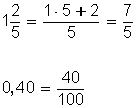
Sumamos (sabiendo que el m.c.m. entre 5 y 100 es 100)
Simplificando, resulta
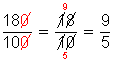
Este resultado se puede convertir en número mixto
Esto
indica que se ocuparon
m de
plástico.
También podemos decir que se ocupó 1,80 metro de plástico (180 dividido 100)
Con base a lo anterior, se concluye que:
Para sumar números mixtos con números decimales es necesario convertirlos a fracciones comunes y después sumar las fracciones equivalentes que tengan igual denominador.
Ver PSU: Matemática: