Operaciones con radicales |
Las raíces que se encuentran dentro del signo radical pueden realizar operaciones entre sí.
Pueden sumarse, restarse, multiplicarse o dividirse si cumplen con determinadas condiciones o reglas.
Suma y resta de radicales
Solamente pueden sumarse (o restarse) dos radicales cuando son radicales semejantes; es decir, si son radicales con el mismo índice e igual radicando (o base subradical).
(Ver: Suma y resta de radicales )
(Ver: Operaciones combinadas )
Producto o multiplicación de radicales
Multiplicar radicales del mismo índice
Se multiplican los radicando (las bases) y se conserva el índice
Multiplicar radicales de distinto índice:
Primero se reducen a índice común y luego se multiplican.
(Ver: Producto o multiplicación de radicales)
Cociente o división de radicales
Dividir radicales del mismo índice
Se dividen los radicando (las bases) y se conserva el índice
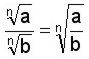
Dividir radicales de distinto índice:
Primero se reducen a índice común y luego se dividen.
(Ver: División de radicales )
Potencia de radicales
(Ver: Potenciación de radicales )
Raíz de un radical
Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva la cantidad subradical.
Ejemplo:
(Ver: Raíz de un radical )
Consiste en quitar los radicales del denominador
, lo cual facilita el cálculo de operaciones como la suma de fracciones.
Podemos distinguir tres casos, para eliminar los radicales del denominador.
a)
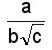Se multiplican el numerador y el denominador por
.
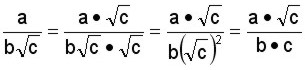
b)
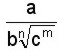Se multiplican el numerador y el denominador por
.
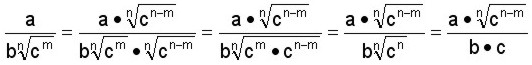c)
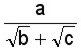
y en general cuando el denominador sea un
binomio con al menos un radical, se multiplican el numerador y denominador por el conjugado del denominador. El conjugado es la misma expresión pero con signo contrario.
Ver: Propiedades de las raíces
Ver: Simplificación de radicales
Además, ver, en Internet:
http://www.sectormatematica.cl/ppt/Raices.pps
Ejercicios en
http://www.ematematicas.net/radicales.php?a =