Regularidades numéricas |
En la vida cotidiana se nos presentan muchas situaciones donde aparecen regularidades numéricas o secuencias numéricas (también puede ser secuencia de objetos de forma ordenada).
Para nuestro interés en ejercitar las destrezas matemáticas, la primera y más importante secuencia numérica es la de los números naturales , o sea los números que se utilizan para contar y ordenar objetos: 1, 2, 3, 4, 5, 6, ...
Esta secuencia de los números naturales es la más importante ya que sirve de base para iniciar, siempre desde el 1 (o primer lugar), cualquier otra secuencia dada, pues, como veremos luego, la ubicación en una secuencia es trascendental para los cálculos numéricos (ya se entenderá cuando hablemos de n ).
Veamos otros ejemplos de secuencias numéricas:
• Secuencia de números pares: 2, 4, 6, 8, 10, 12, 14, ...
• Secuencia de números impares: 1, 3, 5, 7, 9, 11, 13, ...
• Secuencia de múltiplos de 4: 4, 8, 12, 16, 20, 24, 26, ...
• Secuencia de cuadrados de los números naturales: 1, 4, 9, 16, 25, 36, ...
• Secuencia de cubos de los números naturales: 1, 8, 27, 64, 125, ...
• Secuencia de potencias de 2: 2, 4, 8, 16, 32, ...
Estas secuencias numéricas se denominan
sucesiones
.
Entonces:
Una sucesión de números reales es una secuencia ordenada de números reales que sigue una determinada ley de formación.
Los números que forman la sucesión se denominan términos . Todas las sucesiones tienen un primer término y cada término tiene un siguiente. Las sucesiones se nombran con una letra y un subíndice ( n ) cuyo valor depende del lugar que el término ocupa en la sucesión (ese valor empieza siempre en 1, y sigue 2, 3 ,4 ,5, 6, 7, etcétera):
De este modo: a 1 , a 2 , a 3 , a 4 , ...
Término general
El término general de una sucesión es una expresión (fórmula o patrón o regla) que permite conocer el valor de cualquiera de los términos en función del lugar que ocupa. Se expresa mediante a n .
Ejemplo: Si el término general de una sucesión es
a
n
= n
2
+ 1
Para obtener un término cualquiera, se sustituye
n
por el valor del lugar que ocupa el término en la sucesión. Así, a modo de ejemplo, el tercer término será:
a
3
= 3
2
+ 1 = 9 + 1 = 10
Así, por ejemplo, la serie
1, 3, 5, 7, . . .
son los números definidos por la fórmula
2
n
– 1
, pues si
n
es reemplazado por los números naturales, 1, 2, 3, 4, . . . se genera la serie dada.
El siguiente cuadro sirve para comprobar lo anterior:
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
. . . |
100 |
. . . |
k |
|
2 n - 1 |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
|
199 |
|
|
Si se desea saber el número de la serie que ocupa la décima posición se reemplaza n = 10 en la fórmula 2 n – 1.
(2 • 10) − 1 = 19
Nota importante
Tener en cuenta que la expresión 2 n – 1 no es lo mismo que la expresión 2n – 1
Otro ejemplo. Completa la tabla con la serie numérica que genera la fórmula 4 n + 3 .
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
. . . |
100 |
. . . |
k |
|
4n + 3 |
7 |
11 |
15 |
19 |
23 |
27 |
31 |
|
|
|
|
|
|
Determinación de la fórmula
Hasta aquí hemos mostrado ejemplos o ejercicios con la fórmula ya establecida o determinada (2 n – 1 y 4 n + 3 ).
En los ejercicios de regularidades numéricas se trata de encontrar la fórmula (patrón o regla) de formación de una sucesión.
Veamos, como ejemplo 1, el siguiente caso, que se da en un contexto geométrico :
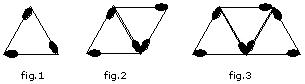
¿Cuántos palitos de fósforos se necesitan para llegar a formar la figura 23 en esta sucesión?
Para saber cuantos fósforos necesitamos para formar la figura 23 (o vigésimo tercera) podríamos recurrir al siguiente cuadro:
| Figura |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
. . . |
100 |
. . . |
n |
|
Fósforos usados |
3 |
5 |
7 |
|
|
|
|
|
|
|
|
|
|
Y completarlo, sumando 2 fósforos cada vez, hasta llegar al espacio Figura 23.
Pero no es necesario completar el cuadro para saber cuántos fósforos necesitamos para armar la figura 23. Para ello debemos determinar la fórmula general que nos dará la respuesta de inmediato.
Analicemos:
Para armar la figura 1 se necesitan 3 fósforos, pero 3 = 2 • 1 + 1
Para armar la figura 2 se necesitan 5 fósforos, pero 5 = 2 • 2 + 1
Para armar la figura 3 se necesitan 7 fósforos, pero 7 = 2 • 3 + 1
Como vemos, el término general es 2 n donde el 2 indica el número de fósforos que debe agregarse cada vez que se avanza en la construcción de las figuras y la n indica (empezando desde la 1) el número de la figura, todo eso más 1; por lo tanto, la fórmula o patrón está dada por 2 n + 1.
Conocida esta fórmula 2 n + 1 reemplazamos simplemente la n por el 23 y sabemos de inmediato que
(2 • 23) +1 nos da 46 + 1 = 47
Por lo tanto, para la figura 23 se necesitarán 47 fósforos.
Ejemplo 2.
Determina la fórmula que genera la serie numérica de la cantidad de fósforos utilizados para construir la figura formada por un número dado de cuadrados, como se muestra en las figuras
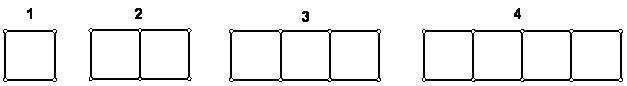
Veamos:
|
Nº de cuadrados |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
. . . |
n |
|
Nº de fósforos |
4 |
7 |
10 |
13 |
|
|
|
|
|
Para armar el cuadrado 1 se necesitan 4 fósforos, pero 4 = 3 • 1 + 1
Para armar el cuadrado 2 se necesitan 7 fósforos, pero 7 = 3 • 2 + 1
Para armar el cuadrado 3 se necesitan 10 fósforos, pero 10 = 3 • 3 + 1
Para armar el cuadrado 4 se necesitan 13 fósforos, pero 13 = 3 • 4 + 1
Partiendo desde el cuadrado 1 necesitamos 3 fósforos cada vez para armar el siguiente, por lo tanto, el término general será
3
n
+ 1
Ejemplo 3
El ejercicio de regularidad numérica puede estar dado solo mediante relaciones numéricas, como en el siguiente ejemplo:
Dadas las siguientes igualdades:
3 2 = 1 2 + 4 • 1 + 4
4 2 = 2 2 + 4 • 2 + 4
Entonces 100 2 será = a: ¿?
Según estas igualdades, cada base de la potencia cuadrática de la derecha tiene 2 unidades menos que cada base de la potencia cuadrática de la izquierda, por lo tanto, nuestro resultado debe empezar con 98 2 (obtenido haciendo 100 – 2); a continuación viene la multiplicación de 4 con el mismo número obtenido anteriormente (es decir: 4 • 98) y finalmente le agregamos el número 4, por lo tanto:
100 2 = 98 2 + 4 • 98 + 4
Ver: PSU: Matemática,
Ejercicios
Hallar el término
a. 9º de la secuencia 7, 10, 13, . . . ...............................................
b. 12º de la secuencia 5, 10, 15, . . . ..............................................
c. 48º de la secuencia 9, 12, 15, . . . ..............................................
d. 63º de la secuencia 3, 10, 17. . . . ..............................................
e. 12º de la secuencia 11, 6, 1, . . . ..............................................
f. 28º de la secuencia 19,12, 5, . . . ...............................................
Determina la fórmula que genera las siguientes series numéricas
a. serie 10, 12, 14, 16, . . . ...............................................
b. serie 10, 13, 16, 19. . . . ..............................................
c. serie 20, 25, 30, 35, . . . ..............................................
d. serie 115, 125, 135, 145. . . . ..............................................
e. serie -10, -4, 2, 8, . . . ..............................................
f. serie 5, 8, 11, 14, . . . ...............................................
Fuentes Internet:
http://www.educarchile.cl/Portal.Base/Web/VerContenido.aspx?GUID=123.456.789.000&ID=133204
www.geolay.com/modulos_primero/mat_reg-numericas.doc
http://www.comenius.usach.cl/webmat2/actividades/mineduc1-1.htm
Para practicar ir a:
http://www.comenius.usach.cl/webmat2/actividades/unidad1-actividades.htm

