Teorema General de Pitágoras

Según el Teorema de Pitágoras , aplicado exclusivamente a los triángulos rectángulos, el cuadrado del valor de la hipotenusa (generalmente “c”) es igual a la suma de los cuadrados de los catetos (por lo general, a y b ).

Es la conocida fórmula

c ² = a ² + b ²

para triángulos rectángulos.

Ojo con esto: esta fórmula permite calcular el valor de cualquiera de los lados, pero, por ejemplo, si es alguno de los catetos, la ecuación debe desarrollarse y cambian los signos.

Por ejemplo, si deseamos conocer a ² : la fórmula queda:

a ² = c ² - b ²

Pero, ¿qué sucede con los triángulos que no son rectángulos?

En ellos, también se puede hallar el valor del cuadrado de un lado, solo que debe aplicarse el Teorema de Pitágoras con una variante: conocida con el nombre de Teorema General de Pitágoras , que se puede usar para cualquier triángulo, sea rectángulo o no lo sea.

Para aplicar el Teorema General de Pitágoras hay que definir o conocer el ángulo que se opone al lado que se desea conocer: definir si es ángulo agudo o ángulo obtuso .

Lado opuesto a un ángulo agudo

Si tenemos un triángulo acutángulo y queremos hallar el cuadrado de uno de sus lados; por ejemplo, el lado "a" —opuesto al vértice A— que en este caso es la hipotenusa, trazaremos la altura (h) sobre cualquiera de los otros dos lados.

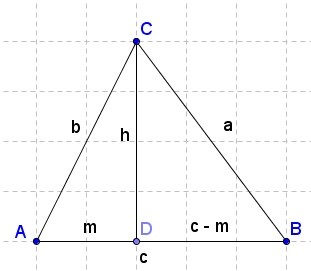
En nuestra figura, trazamos la altura sobre el lado "c" (trazo CD) y al trazo AD lo llamamos "m" (nótese que “m” es la proyección del lado "b" sobre "c").

El trazo DB será entonces c – m

Como vemos, la altura CD divide el triángulo ABC en dos triángulos rectángulos: ADC y CDB.

Al triángulo rectángulo CDB, cuyos lados son a, h y c - m , podemos aplicarle el Teorema de Pitágoras :

a ² = h ² + (c - m) ² = h ² + c ² + m ² - 2 c m

Como ADC también es un triángulo rectángulo, cuyos lados son h, b y m , por el Teorema de Pitágoras :

b ² = h ² + m ²

que, resuelto, queda

h ² = b ² - m ²

Sustituyendo, este segundo resultado en la primera expresión tendremos:

a ² = (b ² - m ² ) + c ² + m ² – 2  c m

a ² =  b ² + c ² – 2 c m

Expresión que corresponde al Teorema General de Pitágoras , aplicado a triángulos acutángulos:

"En un triángulo, el cuadrado del lado opuesto a un ángulo agudo es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de uno de esos lados por la proyección del otro lado sobre el anterior". (Recuerde que la proyección se visualiza al trazar la altura sobre uno de los lados conocidos en el triángulo dado.)

Lado opuesto a un ángulo obtuso

Si tenemos un triángulo obtusángulo , para hallar el cuadrado del lado opuesto al ángulo obtuso, trazaremos la altura sobre cualquiera de los otros dos lados.

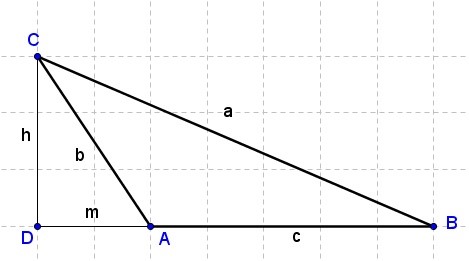
En nuestra figura, trazamos la altura “h” sobre el lado "c" (y nombramos "m" al trazo que es la proyección de "b" sobre la prolongación de "c".

Hecho esto, aparecen dos triángulos rectángulos superpuestos, CDA y CDB, a los que podremos aplicar el Teorema de Pitágoras .

Entonces, CDB triángulo rectángulo, y por el Teorema de Pitágoras:

a ² = h ² + (c + m) ² = h ² + c ² + m ² + 2 c m

Como CDA también es un triángulo rectángulo, y otra vez, por el Teorema de Pitágoras:

b ² = h ² + m ² ⇒     h ² = b ² – m ²

Sustituyendo, el segundo resultado, en la primera expresión, queda:

a ² = (b ² - m ² ) + c ² + m ² + 2 c m

a ² =  b ² + c ² + 2 c m

Expresión que se conoce como Teorema General de Pitágoras , aplicado a triángulos obtusángulos:

"En un triángulo, el cuadrado del lado opuesto a un ángulo obtuso es igual a la suma de los cuadrados de los otros dos lados más el doble producto de uno de esos lados por la proyección del otro lado sobre el anterior". (Recuerde que la proyección se visualiza al trazar la altura sobre uno de los lados conocidos en el triángulo dado.)

Para triángulos rectángulos

En la figura precedente hemos llamado "m" la proyección del lado "b" sobre el "c". Dicha proyección será tanto más pequeña cuanto más próximo a un ángulo recto sea el ángulo opuesto al lado "a".

Cuando dicho ángulo sea de 90° (triángulo rectángulo), la proyección "m" sería nula (m = 0).

Al sustituir (m = 0), en cualquiera de las expresiones anteriores, llegaremos a

a ² =  b ² + c ²

y como en nuestros ejemplos “a” es la hipotenusa, vemos que nos encontramos con el Teorema de Pitágoras para triángulos rectángulos:

c ² = a ² + b ²

Nota:

Tanto el Teorema de Pitágoras como el mismo en su forma General, sirven para calcular las dimensiones de uno de los lados de un triángulo si conocemos al menos el valor de los otros dos.

Cuando la información de un triángulo contiene el valor de algún ángulo y se necesite calcular el valor de alguno de sus lados, o del resto de sus ángulos, debemos recurrir al Teorema de los senos o al Teorema del Coseno.

Ir a: Teorema del seno o de los senos

Ir a: Teorema del coseno o de los cosenos