Teselaciones |
|
Imaginemos a nuestra disposición una provisión infinita de piezas de rompecabezas, pero todas iguales: se dice que la pieza es teselante cuando es posible acoplarlas entre sí sin huecos ni fisuras hasta recubrir por completo el plano; la configuración que en tal caso se obtiene recibe el nombre teselación. |
Las teselaciones han sido utilizadas en todo el mundo desde los tiempo más antiguos para recubrir suelos y paredes, e igualmente como motivos decorativos de muebles, alfombras, tapices, ropas,...
También muchos artistas han utilizado teselaciones en su trabajo: M.C. Escher es, probablemente, el más famoso de todos ellos. El artista holandés se divirtió teselando el plano con figuras de intrincadas formas, que recuerdan pájaros, peces, animales...
Como es fácil de imaginar, la diversidad de las formas de las piezas teselantes es infinita. Los matemáticos y en particular los geómetras se han interesado especialmente por las teselaciones poligonales; incluso las más sencillas de estas plantean problemas colosales.
Algunas teselaciones importantes
Cuando todos los polígonos de la teselación son regulares e iguales entre sí, se dice que la teselación es regular.
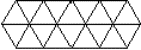
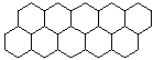
Ahora bien, sólo existen tres teselaciones o mosaicos regulares: la malla de triángulos equiláteros , el reticulado cuadrado como el del tablero de ajedrez y la configuración hexagonal , como la de los paneles.
|
Teselación de Triángulos
|
|
Teselación de Cuadrados
|
|
Teselación de Hexágonos
|
Un movimiento o isometría es una transformación que preserva todas las distancias y por ello preserva el tamaño y la forma. (Nota: iso significa "igual" y metría significa "medida"). La imagen de una figura bajo esta transformación siempre es congruente con la figura original.
Tipos de isometrías en el plano
|
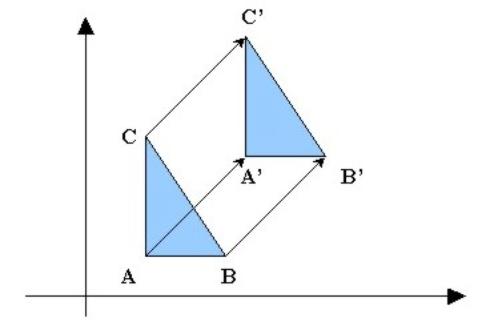
Traslación: Isometría en que todos los puntos se desplazan una distancia fija hacia sus imágenes a lo largo de trayectorias paralelas.
|
|
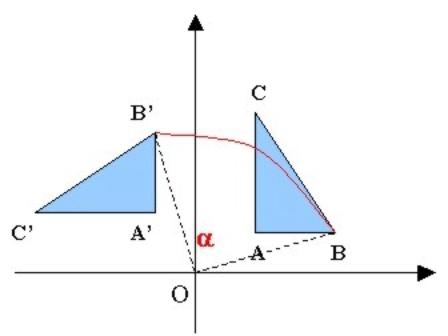
Rotación: Isometría en que todos los puntos giran un ángulo constante con respecto a un punto fijo. El punto fijo se denomina centro de rotación y la cantidad de giro se denomina ángulo de rotación.
O centro de rotación α ángulo de rotación |
|
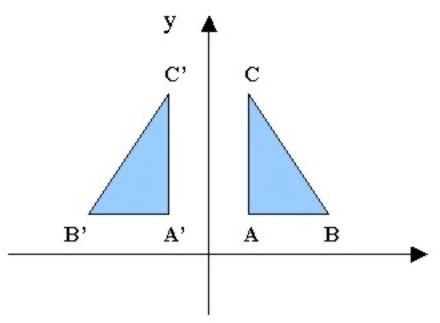
Reflexión: Isometría en que todos los puntos son enviados a sus imágenes reflejadas con respecto a una recta de reflexión , que actúa como espejo.
Eje y actúa como recta de reflexión |
El embaldosado con Transformaciones Isométricas
La simple observación y análisis de embaldosados, nos permite comprobar que estos se construyen sobre la base de transformaciones isométricas, como en los siguientes ejemplos:

|
|
Embaldosado
por traslación
|
|
|
Embaldosado
por rotación
|
|
|
Embaldosado
por reflexión
|
Traslación, Rotación y Reflexión son tres transformaciones isométricas mediante las cuales puede hacerse coincidir una figura consigo misma.
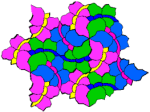
Ejemplos de teselaciones

|

|

|

|

|

|
Ejercicios
|
Pentominos
Alrededor de la piscina de 4 × 7 queremos colocar césped
artificial. Para ello disponemos de piezas que tienen
la forma de los pentominós; en el manual de instrucciones
nos confirman que con las mismas podemos cubrir todo el campo,
sin cortar ni superponer ninguna pieza.
|
|
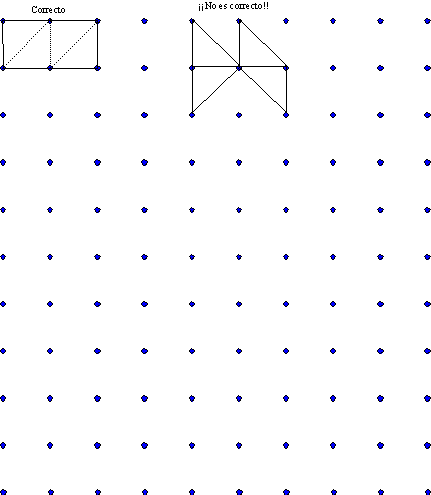
Geoplano
Construir en el geoplano todas las figuras posibles formadas
por 4 triángulos rectángulos de igual superficie, unidos por
los catetos o por la hipotenusa.
|
|
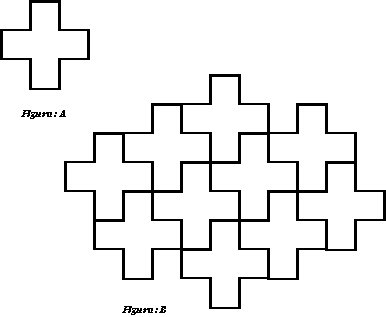
Teselaciones Los trabajadores de la construcción hacen paredes y suelos montando grandes cantidades de cuerpos sólidos geométricos, la mayoría de las veces, idénticos. Muchas aceras, calzadas, zócalos, frisos e incluso paredes completas se hacen con losetas de diferentes tamaños, formas y unidas entre sí en distintas posiciones. A las losetas que cubren una superficie plana y se ajustan bien entre sí, sin dejar huecos ni montarse unas encima de otras, se les llaman teselas. Cuando una superficie se puede cubrir perfectamente en todas las direcciones con este tipo de losetas o teselas, decimos que hemos realizado una teselación. La figura A es un pentominó , con ella podemos rellenar el plano, es decir, podemos hacer una teselación -figura B-. Observen que no deja huecos ni se monta una sobre otra.
Utilizando los polígonos regulares que se dan, investigar
cuál o cuáles de ellos pueden ponerse alrededor de un
vértice sin que dejen huecos ni se monten unos encima de otros.
|
Ver, en Internet:
http://www.geocities.com/SiliconValley/Vista/2212/tesela.html