En un conjunto Universo de referencia un conjunto complementario (o complemento de un conjunto) es otro conjunto que contiene todos los elementos que no están en el conjunto original definido.
Entonces, para poder determinar los elementos de un conjunto complementario, es necesario especificar el Conjunto Universo de referencia.
Veamos un ejemplo:
Si el conjunto universo es
U = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 }
y tenemos dentro el subconjunto
A = { 3, 4, 7, 9, 10, 11 },
entonces el Complementario de A (que se escribe como Ac) respecto del conjunto universo ( U ), está formado por los elementos de este universal que no están en A.
¿Cuáles elementos de U no están en A?
Ac = { 1, 2, 5, 6, 8 }
Los conjuntos A ={ 3, 4, 7, 9, 10, 11 } y Ac ={ 1, 2, 5, 6, 8 } son complementarios.
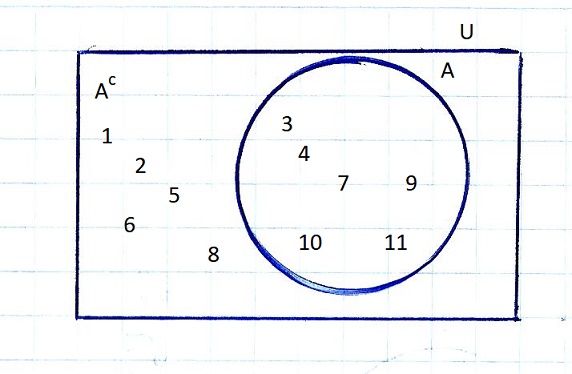
Ejercicio de práctica
Sea U = {x Ε Z │ 1 ≤ x ≤ 11}
Se lee, Conjunto Universo donde x, que pertenece a los enteros, es igual o mayor que 1 e igual o menor que 11.
Entonces, según el enunciado, el Conjunto Universo es
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
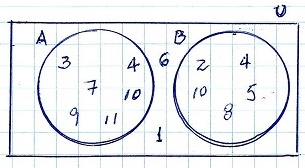
Donde A y B son subconjuntos de U, tales que
Ac ∩ Bc = {1, 6} (Ac interseccion Bc)
A ∩ B = {4, 10} (A intersección B)
B ∩ Ac = {2, 5, 8} (B intersección Ac)
Las operaciones de intersección ( ∩ ) entre los subconjuntos A y B indicadas, respecto al conjunto Universo, nos dan la clave para descubrir los elementos que forman cada subconjunto.
Veamos
Ac intersección Bc
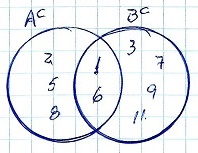
Ac ∩ Bc = {1, 6} indica que los elementos 1 y 6 son comunes a Ac y Bc, que son los complementarios de A y de B, respecto al Universo.
Subconjunto Ac = {1, 2, 5, 6, 8} (los elementos 2, 5 y 8 se descubren luego)
Subconjunto Bc = {1, 3, 6, 7, 9, 11} (los elementos 3, 7, 9 y 11 se descubren luego)
A intersección B
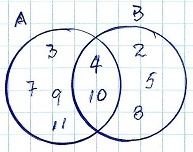
A ∩ B = {4, 10} indica que los elementos 4 y 10 son comunes a los subconjuntos A y B, respecto al Universo.
Subconjunto A = {3, 4, 7, 9, 10, 11} (los elementos 3, 7, 9 y 11 se desubren luego)
Subconjunto B = {2, 4, 5, 8, 10} (los elementos 2, 5 y 8 se descubren luego)
B intersección Ac
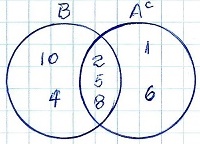
B ∩ Ac = {2, 5, 8}, indica que los elementos 2, 5 y 8 son comunes a los subconjuntos B y Ac, respecto al Universo.
Observación:
El dato más relevante para descubrir los elementos de estos subconjuntos está en la participación en B.
A ∩ B = {4, 10} y B ∩ Ac = {2, 5, 8}, indica que B = {2, 4, 5, 8, 10};
por lo tanto, Bc = {1, 3, 6, 7, 9, 11}.
Y la participación en Ac
Ac ∩ Bc = {1, 6} y B ∩ Ac = {2, 5, 8} lo cual indica que Ac = {1, 2, 5, 6, 8};
Por lo tanto, A = {3, 4, 7, 9, 10, 11}
Entonces, a partir del
Conjunto Universo U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
Tenemos
Subconjunto Ac = {1, 2, 5, 6, 8} , complementario de subconjunto A = {3, 4, 7, 9, 10, 11}
Subconjunto Bc = {1, 3, 6, 7, 9, 11}, complementario de subconjunto B = {2, 4, 5, 8, 10}
Lo que podemos comprobar
∩ = intersección (elementos que están en ambos subconjuntos)
Ac ∩ Bc = {1, 2, 5, 6, 8} Ⴖ {1, 3, 6, 7, 9, 11} = {1, 6}
A ∩ B = {3, 4, 7, 9, 10, 11} Ⴖ {2, 4, 5, 8, 10} = {4, 10}
B ∩ Ac = {2, 4, 5, 8, 10} Ⴖ {1, 2, 5, 6, 8} = {2, 5, 8}






