Reconocer el total de partes en una fracción |
Si observas los
siguientes dibujos podrás notar que las fracciones que las representan forman
un total igual a la unidad (1).
Deduce esto por ti mismo observando
atentamente las siguientes representaciones de fracciones.
|
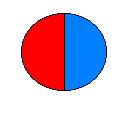
Este dibujo está dividido en dos partes. La parte roja es una parte pintada, de dos partes , que tú ya sabes que se representa como ½. A su vez, la parte azul es también una parte pintada, de dos partes , o sea, ½. Por lo tanto, la circunferencia tiene dos medios (2/2) .
|
|
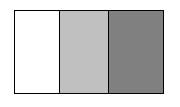
Este dibujo está dividido en tres partes . La parte blanca es 1/3; la parte gris es 1/3; la parte gris más oscura es también 1/3 del total, por lo tanto, el rectángulo tiene tres tercios (3/3).
= 1 (1, porque está pintada toda la figura, o sea, el entero) |
|
Este dibujo está dividido en cuatro partes . La parte calipso es ¼ del total; la parte celeste es ¼ del total; la parte azulina es también ¼ del total; y la parte azul más oscura es ¼, por lo tanto, el rectángulo entero (la unidad) tiene cuatro cuartos (4/4).
|
... y así, sucesivamente...
De acuerdo estos ejemplos se pueden sacar dos conclusiones:
Las fracciones que tienen el numerador igual a su denominador son iguales a 1 . Se llaman fracciones iguales a la unidad . Si el entero está dividido en un número determinado de partes, el total corresponderá a la suma del número de partes en que se dividió el entero. Por ejemplo: si el entero se dividió en dos partes, significa que tiene dos medios; si el entero se dividió en ochos partes significa que el entero tiene 8/8 (ocho octavos), etc.