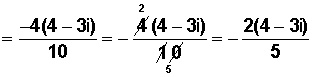Anteriormente, conocimos los números imaginarios, y definimos la unidad imaginaria (i) como la raíz cuadrada del número real negativo 1 ( ), y vimos cómo, a partir de esa unidad, podemos expresar la raíz cuadrada de los números negativos.

Pues bien, sabido esto, podemos definir qué son los números complejos:

Un número complejo (z) está formado por la suma de un número real (a) más un número real (b) multiplicado éste por la unidad imaginaria (i), de la forma:

z = a + b * i   o  solo  z = a + bi

forma denominada binómica (o canónica), y donde el número real (a) se llama parte real del número complejo y el número real (b) se llama parte imaginaria del número complejo, e (i) es la unidad imaginaria.

Aparte de la forma binómica (z = a + b * i), existen otras formas de representar un número complejo. Estas otras formas son: como par ordenado o como representación gráfica, siendo posible pasar de una a otra.

En este apartado, nos dedicaremos exclusivamente a los números complejos expresados en su forma binómica.

Resumiendo, diremos que los números complejos se inventaron, a partir de una unidad imaginaria, para que las raíces negativas que aparecen en las ecuaciones de segundo grado tuviesen solución.

Debemos agregar que también hay ecuaciones en las cuales los componentes se indican como número complejo.

Los números complejos se pueden sumar, restar,  multiplicar o dividir, tal como los binomios algebraicos.

Sumar y restar complejos en forma binómica

Para sumar o restar dos números complejos, se suman o restan entre sí las partes reales y entre sí las partes que incluyen lo imaginario.

Veamos un ejemplo:

Tenemos dos complejos (z y w) expresados en su forma binómica:

Hagamos la suma:

Ahora, hagamos la resta:

Un ejercicio para muestra: Sumar y restar los números complejos:

z = 2 + 6i

y

w = 1 - 3i

Primero la suma:

z + w =

(2 + 6i) + (1 – 3i) = (2 + 1) + (6i + ( - 3i) ) = 3 + 3i

Ahora la resta:

z – w =

(2 + 6i) – (1 – 3i) = (2 – 1) + (6i – (- 3i) ) = 1 + 9i

Multiplicar complejos en forma binómica

z = 2 + 6i

y

w = 1 - 3i

z * w =

Se multiplica igual que binomio por binomio, pero recordar que i²  = – 1

(2 + 6i) (1 – 3i) = (2 *1) – (2 * 3i) + (6i * 1) – (6i * 3i) =

= 2 – 6i +  6i – (18)i2  = 2 – (18)( - 1) = 2 + 18 = 20

Dividir o Cociente de complejos en forma binómica

Usando los mismos números complejos del ejemplo anterior, haremos una división entre ellos para explicar su desarrollo, como si fuera una división entre binomios:

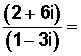
Hagamos un análisis previo: la presencia de números imaginarios (6i y 3i) nos indica que tenemos radicales tanto en el numerador como en el denominador de esta fracción con números complejos.

Recuerden que 6i es el imaginario que corresponde a

Y que 3i corresponde a

según aprendimos al estudiar los números imaginarios.

Entonces, como tenemos radicales en el denominador, debemos racionalizar (eliminar el radical del denominador). Para ello, amplificamos la fracción completa por el conjugado (el inverso, que es 1 + 3i) del denominador:

De nuevo, recordar que i² = – 1.

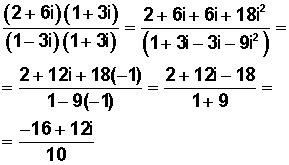
Resultado que podemos factorizar: