Par de fuerzas

Un par de fuerzas es un sistema de dos fuerzas paralelas , de igual intensidad y de sentido contrario, que produce un movimiento de rotación.

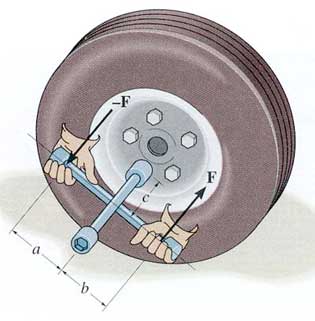
Cuando alguien utiliza una llave para quitar la rueda de un coche (automóvil), aplica dos fuerzas iguales y de sentido contrario.

Se observa que la llave no experimenta movimiento de traslación alguno, es decir, no se desplaza, pero sí gira bajo la acción del par de fuerzas .

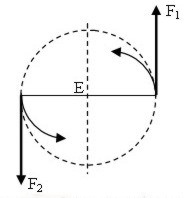
Un par de fuerzas produce un movimiento de rotación,

Aunque la resultante de las fuerzas del par es nula ( R = F1 –  F2 = 0 ), sin embargo, los momentos de cada fuerza del par, con respecto al punto E ,  suman su capacidad de producir un giro , por ello el efecto de un par de fuerzas es producir una rotación .

El volante (manubrio) de un carro (automóvil) es una aplicación práctica de un par de fuerzas.

También lo son las regaderas que se usan en los jardines para regar el césped.

Entonces, diremos que un par de fuerzas , es un sistema formado por dos fuerzas de la misma intensidad o módulo , pero de dirección contraria, capaces de producir en su momento una rotación.

Sacamos los pernos apoyados en un par de fuerzas.

Entonces, un par de fuerzas queda caracterizado por su momento (M).

El valor del momento de un par de fuerzas es igual al producto de una de las fuerzas por la distancia que las separa:

Esto es,

M = F1d = F2d

La distancia que separa las fuerzas recibe el nombre de brazo del par

Ejemplo:

Calcular el valor del momento de un par de fuerzas cuya intensidad es 5 N si el brazo del par mide 2 m.

Solución:

M = F • d  =  5N • 2m  =  10Nm

Ejemplos comunes de pares de fuerza

En nuestra vida cotidiana encontramos numerosos aparatos o realizamos movimiento que se hacen aplicando un par de fuerzas.

Entre otros tenemos:

Destornillador

Sacacorchos

Utilizamos el sacacorchos, pero el trabajo lo realiza un par de fuerzas.

Apertura o cierre de una llave (grifo)

Ajustador de brocas de un taladro.

Batidora manual

Volante de un vehículo

Ejercicios.

Calcular el valor del momento de los siguientes pares de fuerzas:

1) 8N  separadas 8m.

2) 5N separadas 10m.

3) 6N separadas 3m.

4) 12N separadas 4m.

5) 10N separadas 6m.

6) 20N separadas 5m.

7) 9N separadas 6m.

8) 7N separadas 3m.

Ver: Sistemas de fuerzas paralelas

Ver: Sistema de fuerza angulares

Ver: Torque o Momento de una fuerza.

Ver: Sistemas de fuerzas colineales

Fuentes Internet:

http://recursostic.educacion.es/secundaria/edad/4esofisicaquimica/impresos/quincena3.pdf

http://recursostic.educacion.es/secundaria/edad/4esofisicaquimica/4quincena3/4q3_contenidos_1a.htm

Ver:

http://fisicaparatodo.files.wordpress.com/2011/02/vectores-no-colineales1.pdf

http://fisicacom.host22.com/VECTORES.HTML

http://recursostic.educacion.es/secundaria/edad/4esofisicaquimica/impresos/quincena3.pdf

http://quimicayalgomas.com.ar/fisica/sistemas-de-fuerzas-resultante

Ver Youtube:

http://www.youtube.com/watch?v=UsytbVG6GtI

Desartrollar este ejemplo

http://www.youtube.com/watch?v=1BGub9Sqn5g&feature=fvwrel