Romboide: área y perímetro

El romboide es un paralelógramo (un tipo de cuadrilátero ) que no es ni rombo ni rectángulo ; es decir, un paralelógramo que tiene dos pares de lados paralelos e iguales entre sí (a = c; y b = d en la figura) formando dos pares de ángulos también iguales entre sí. (lados y ángulos iguales dos a dos).

Área del romboide

El área del romboide se obtiene multiplicando la base por altura .

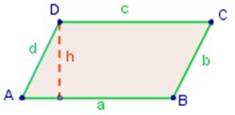
En este caso, si tomamos como base el lado a , tenemos;

A = a · h

Ejercicio

Calcular el área de un romboide cuyos pares de lados miden 4 y 5 cm y su altura mide 3,5 cm.

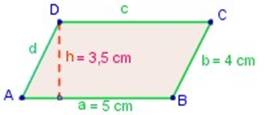
A = a . h

A = 5 · 3,5 = 17,5 cm2

Perímetro del romboide

El perímetro del romboide es igual a la suma de las longitudes de sus cuatro lados .

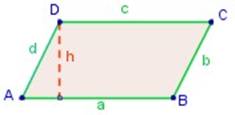
P = 2 · a + 2 · b

P = 2 · (a + b)

Ejercicio 1

Calcular el perímetro de un romboide cuyos pares de lados miden de 4 y 5 cm de lados y su altura mide 3,5 cm.

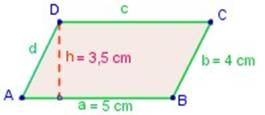
P = 2 · (5 + 4) = 18 cm

¿Puedes calcular su área?

Ejercicio 2

En el romboide ABCD , trazo DC = 12 cm ; trazo AD = 5 cm y trazo AE = 3 cm

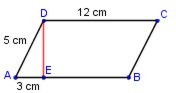
Hagamos un análsis  de los datos que nos dan:

Si el trazo DC mide 12 cm, entonces el trazo AB también mide 12 cm.

El trazo DE corresponde a la altura (h) del romboide y como es un dato necesario para calcular el área debemos averiguar cuánto vale h .

Para ello, vemos que el triángulo rectángulo AED tiene por hipotenusa 5 cm y uno de los catetos mide 3 cm . El otro cateto corresponde a la altura (h) del romboide.

Calculamos el valor de ese cateto (h) usando el Teorema de Pitágoras :

c ² = a ² + b ²

5 ² = 3 ² + b ²

25 = 9 + b ²

–b ² = 9 – 25

–b ² = –16   /–1

b ² = 16

b =  √¯16

b = 4

La altura (h) mide 4 cm .

Ahora podemos preguntar:

¿Cuál es su perímetro?

P = 2 . (a + b)

P = 2(12 + 5)

P = 34 cm

¿Cuál es su área?

A = a . h

a = 12 cm

h = 4 cm

A = 12 . 4 = 48 cm ²

Fuente Internet:

http://www.ditutor.com/geometria/area_romboide.html

Ver:

http://www.genmagic.org/mates1/ap1c.swf

Todo sobre cuadriláteros

http://www.geolay.com/cuadrilateros.htm