En triángulos, calcular ángulos desconocidos |
Para calcular cualquier ángulo desconocido en un triángulo es necesario tener los siguientes conocimientos previos:
1) Clasificación de triángulos según la medida de sus lados (equilátero, isósceles, escaleno) y según la medida de sus ángulos (acutángulo, rectángulo, obtusángulo).
|
2) Todo ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores no adyacentes a él.
|
|
|
|
|
3) En todo triángulo la suma de sus ángulos interiores es siempre 180º.
4) La suma de dos ángulos adyacentes suplementarios es siempre un ángulo extendido, es decir, 180º
5) Elementos secundarios del triángulo (altura, bisectriz, simetral, etc.)
6) Ángulos entre paralelas (ángulos alternos, correspondientes, conjugados, etc.)
Conociendo estos conceptos básicos de geometría se pueden resolver problemas como los siguientes:
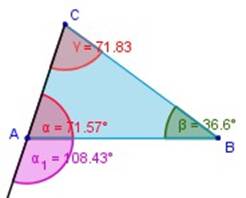
Problema 1)
Calcular la medida de γ y γ1
Para resolver este ejercicio se deben usar dos teoremas de los mencionados anteriormente:
Primero se debe calcular el ángulo interior del triángulo (se tienen la medida de dos ángulos y se puede averiguar el tercero).
α + β + γ = 180º (suma de ángulos interiores, siempre = 180º)
45º + 63,43º + x = 180º
x + 108,43º = 180º
x = 180º ─ 108,43º
x = 71,57º
x = γ
Por lo tanto, γ = 71,57º
Con este resultado se puede ahora calcular el ángulo exterior (el ángulo exterior y el ángulo interior adyacente a él suman 180º )
γ + γ1 = 180º (suma de ángulos adyacentes suplementarios = 180º)
71,57º + γ1 = 180º
γ1 = 180º ─ 71,57º
γ1 = 108,43º
Problema 2)
Se tiene un ∆ ABC equilátero ¿Cuánto mide un ángulo exterior?
Un triángulo equilátero es el que tiene todos sus lados de igual medida y por ende todos sus ángulos de igual medida; es decir, 60º cada uno (60 · 3 = 180º).
Si un ángulo interior mide 60º significa que su ángulo exterior mide 120º porque 180 – 60 = 120º (el ángulo interior y el ángulo exterior son suplementarios; o sea, miden 180º porque forman un ángulo extendido).
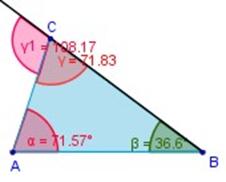
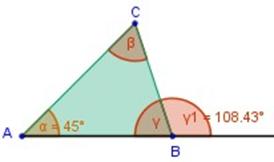
Problema 3)
Calcular el valor de β en el triángulo siguiente:
|
Primero, calculamos ángulo γ en el vértice B:
180º – 108,43º = 71,57º (son suplementarios)
γ = 71,57º
Calcular β : ángulos dentro del triángulo suman 180º:
α + γ + β = 180º
45º + 71,57º + β = 180º
116,57 + β = 180º
β = 180º ─ 116,57
β = 63,43º
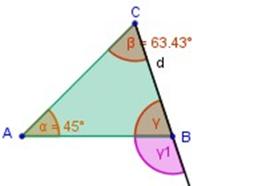
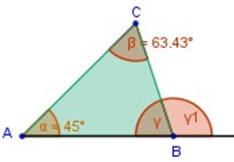
Problema 4)
Calcular el valor de γ1 en el triángulo siguiente:
|
Calculamos ángulo γ en vértice B:
α + γ + β = 180º
45º + γ + 63,43º = 180º
45º + 63,43º + γ = 180º
108,43º + γ = 180º
γ = 180º ─ 108,43º
= 71,57º
El ángulo γ y el ángulo γ1 son adyacentes suplementarios, por lo que suman 180º
Entonces:
γ + γ1 = 180º
71,57º + γ1 = 180º
γ1 = 180º – 71,57º
γ1 = 108,43º