Sistema Métrico Decimal |
Medidas y magnitudes
Para adentrarnos en el tema, es necesario aclarar o definir estos conceptos:
Una magnitud es cualquier propiedad que se puede medir numéricamente .
Medir es comparar una magnitud con otra que llamamos unidad .

|
| Medir es comparar. |
La medida es el número de veces que la unidad está contenida en la magnitud.
Si queremos medir la longitud de una pieza, lo primero que debemos hacer es elegir la unidad de medida, en este caso la más apropiada sería el metro .
Origen y destino
En el pasado cada país y en algunos casos cada región usaban unidades de medidas diferentes, esta diversidad dificultó las relaciones comerciales entre los pueblos. Para acabar con esas dificultades, en 1791, tras la Revolución Francesa , la Academia de Ciencias de París propuso el Sistema Métrico Decimal .
Progresivamente fue adoptado por todos los países, a excepción de los de habla inglesa, que se rigen por el Sistema Inglés o Sistema Imperial Británico .
En España su empleo se hizo oficial desde 1849, aunque sobre todo en el ámbito agrario ha coexistido con las medidas tradicionales .
El sistema métrico decimal de la Revolución Francesa se ha convertido hoy en día en un sistema más moderno, más universal y más completo, conocido como Sistema Internacional de Unidades .
Cómo funciona el Sistema Métrico Decimal
El Sistema Métrico Decimal es un sistema de unidades en el cual los múltiplos y submúltiplos de una unidad de medida están relacionadas entre sí por múltiplos o submúltiplos de 10 .
El Sistema Métrico Decimal lo utilizamos para medir las siguientes magnitudes :

|
| Longitud, el largo de las cosas. |
Medidas de longitud
La unidad de las medidas de longitud es el metro (m).
Los múltiplos del metro se forman anteponiendo a la palabra metro, los prefijos griegos Deca, Hecto y Kilo, que significan diez, cien y mil, respectivamente.
Los submúltipos del metro se forman anteponiendo los prefijos griegos deci, centi y mili, que significan décima, centésima y milésima parte, respectivamente.
Los múltiplos y submúltiplos del metro aumentan y disminuyen de diez en diez , y son:
Kilómetro (Km)
Hectómetro (Hm)
Decámetro (Dm)
metro (m)
decímetro (dm)
centímetro (cm)
milímetro (mm)
En el cuadro siguiente mostramos las equivalencias entre ellas:
|
|
(Km) |
(Hm) |
(Dm) |
(m) |
(dm) |
(cm) |
(mm) |
|
(Km) |
1 |
10 |
100 |
1.000 |
10.000 |
100.000 |
1.000.000 |
|
(Hm) |
0,1 |
1 |
10 |
100 |
1.000 |
10.000 |
100.000 |
|
(Dm) |
0,01 |
0,1 |
1 |
10 |
100 |
1.000 |
10.000 |
|
(m) |
0,001 |
0,01 |
0,1 |
1 |
10 |
100 |
1.000 |
|
(dm) |
0,0001 |
0,001 |
0,01 |
0,1 |
1 |
10 |
100 |
|
(cm) |
0,00001 |
0,0001 |
0,001 |
0,01 |
0,1 |
1 |
10 |
|
(mm) |
0,000001 |
0,00001 |
0,0001 |
0,001 |
0,01 |
0,1 |
1 |
Como debe leerse el cuadro:
Por ejemplo:
1 Km es igual a 10 Hm
1 Km es igual a 100 Dm
1 Km es igual a 1.000 m
1 Km es igual a 10.000 dm
1 Km es igual a 100.000 cm
1 Km es igual a 1.000.000 mm
Para cada mediida es lo mismo.
El cuadro, de aparente complejidad, nos permite hacer fácilmente la conversión entre cualquiera de las medidas.

|
Veamos un ejemplo:
Fijemos la atención en los cuadros coloreados.
Si nos dan una medida en decímetros (dm) y la multiplicamos por 0,1 tendremos los dm convertidos en metros (m).
En sentido inverso, si nos dan una medida en metros (m) y la dividimos por 0,1 , tendremos los metros convertidos en decímetros (dm).
Este juego de multiplicar por los valores de la tabla en sentido horizontal o dividir por los valores en sentido vertical se aplica a cualquiera de las medidas.
Ejercicios:
Convertir 4.000 cm a hectómetros (Hm), a decámetros (Dm) y a milímetros (mm)
4.000 • 0,0001 = 0,4 Hm
4.000 • 0,001 = 4 Dm
4.000 • 10 = 40.000 mm
También podemos hacerlo dividiendo por los valores en sentido vertical:

Para no que no se preste a confusión, debemos señalar que, como norma, se aconseja lo siguiente:
Para convertir una magnitud grande a otra más pequeña, se haga una multiplicación.
Para convertir una magnitud pequeña a otra más grande, se haga una división.
Ver: Para resolver problemas de conversión de medidas en el Sistema Métrico Decimal
Ir a: Metrología lineal o dimensional

|
Medidas de masa (peso).
La unidad de las medidas de masa (peso) es el gramo .
Los múltiplos y submúltiplos del gramo aumentan y disminuyen de diez en diez y son:
Kilógramo (Kg)
Hectógramo (Hg)
Decágramo (Dg)
gramo (g)
decígramo (dg)
centígramo (cg)
milígramo (mg)
En el cuadro siguiente mostramos las equivalencias entre ellas:
|
|
(Kg) |
(Hg) |
(Dg) |
(g) |
(dg) |
(cg) |
(mg) |
|
(Kg) |
1 |
10 |
100 |
1.000 |
10.000 |
100.000 |
1.000.000 |
|
(Hg) |
0,1 |
1 |
10 |
100 |
1.000 |
10.000 |
100.000 |
|
(Dg) |
0,01 |
0,1 |
1 |
10 |
100 |
1.000 |
10.000 |
|
(g) |
0,001 |
0,01 |
0,1 |
1 |
10 |
100 |
1.000 |
|
(dm) |
0,0001 |
0,001 |
0,01 |
0,1 |
1 |
10 |
100 |
|
(cg) |
0,00001 |
0,0001 |
0,001 |
0,01 |
0,1 |
1 |
10 |
|
(mg) |
0,000001 |
0,00001 |
0,0001 |
0,001 |
0,01 |
0,1 |
1 |
Como debe leerse el cuadro:
Por ejemplo:
1 Kg es igual a 10 Hg
1 Kg es igual a 100 Dg
1 Kg es igual a 1.000 g
1 Kg es igual a 10.000 dg
1 Kg es igual a 100.000 cg
1 Kg es igual a 1.000.000 mg
Para cada mediida es lo mismo.
El cuadro, de aparente complejidad, nos permite hacer fácilmente la conversión entre cualquiera de las medidas.
Veamos un ejemplo:
Fijemos la atención en los cuadros coloreados.
Si nos dan una medida en decígramos (dg) y la multiplicamos por 0,1 tendremos los dg convertidos en gramos (g).
En sentido inverso, si nos dan una medida en gramos (g) y la dividimos por 0,1 , tendremos los gramos convertidos en decígramos (dg).
Este juego de multiplicar por los valores de la tabla en sentido horizontal y dividir por los valores en sentido vertical se aplica a cualquiera de las medidas.
Ejercicios:
Convertir 4.000 cg a hectógramos (Hg), a decágramos (Dg) y a milígramos (mg)
4.000 • 0,0001 = 0,4 Hg
4.000 • 0,001 = 4 Dg
4.000 • 10 = 40.000 mg
También podemos hacerlo dividiendo por los valores en sentido vertical:
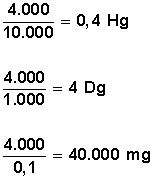
Para no que no se preste a confusión, debemos señalar que, como norma, se aconseja lo siguiente:
Para convertir una magnitud grande a otra más pequeña, se haga una multiplicación.
Para convertir una magnitud pequeña a otra más grande, se haga una división.
Ver: Para resolver problemas de conversión de medidas en el Sistema Métrico Decimal
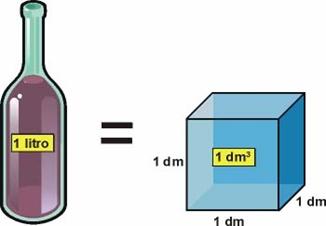
|
| Equivalencia entre capacidad y volumen. |
Medidas de capacidad
La unidad de las medidas de capacidad es el litro .
Los múltiplos y submúltiplos del litro aumentan y disminuyen de diez en diez y son:
Kilólitro (Kl)
Hectólitro (Hl)
decálitro (Dl)
litro (l)
decílitro (dl)
centílitro (cl)
milílitro (ml)
En el cuadro siguiente mostramos las equivalencias entre ellas:
|
|
(Kl) |
(Hl) |
(Dl) |
(l) |
(dl) |
(cl) |
(ml) |
|
(Kl) |
1 |
10 |
100 |
1.000 |
10.000 |
100.000 |
1.000.000 |
|
(Hl) |
0,1 |
1 |
10 |
100 |
1.000 |
10.000 |
100.000 |
|
(Dl) |
0,01 |
0,1 |
1 |
10 |
100 |
1.000 |
10.000 |
|
(l) |
0,001 |
0,01 |
0,1 |
1 |
10 |
100 |
1.000 |
|
(dl) |
0,0001 |
0,001 |
0,01 |
0,1 |
1 |
10 |
100 |
|
(cl) |
0,00001 |
0,0001 |
0,001 |
0,01 |
0,1 |
1 |
10 |
|
(ml) |
0,000001 |
0,00001 |
0,0001 |
0,001 |
0,01 |
0,1 |
1 |
Como debe leerse el cuadro:
Por ejemplo:
1 Kl es igual a 10 Hl
1 Kl es igual a 100 Dl
1 Kl es igual a 1.000 l
1 Kl es igual a 10.000 dl
1 Kl es igual a 100.000 cl
1 Kl es igual a 1.000.000 ml
Para cada medida es lo mismo.
El cuadro, de aparente complejidad, nos permite hacer fácilmente la conversión entre cualquiera de las medidas.
Veamos un ejemplo:
Fijemos la atención en los cuadros coloreados.
Si nos dan una medida en decílitros (dl) y la multiplicamos por 0,1 tendremos los dl convertidos en litros (l).
En sentido inverso, si nos dan una medida en litros (l) y la dividimos por 0,1 , tendremos los litros convertidos en decílitros (dl).
Este juego de multiplicar por los valores de la tabla en sentido horizontal y dividir por los valores en sentido vertical se aplica a cualquiera de las medidas.
Ejercicios:
Convertir 4.000 cl a hectólitros (Hl), a decálitros (Dl) y a milílitros (ml)
4.000 • 0,0001 = 0,4 Hl
4.000 • 0,001 = 4 Dl
4.000 • 10 = 40.000 ml
También podemos hacerlo dividiendo por los valores en sentido vertical:
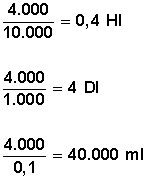
Para no que no se preste a confusión, debemos señalar que, como norma, se aconseja lo siguiente:
Para convertir una magnitud grande a otra más pequeña, se haga una multiplicación.
Para convertir una magnitud pequeña a otra más grande, se haga una división.
Ver: Para resolver problemas de conversión de medidas en el Sistema Métrico Decimal
|
| Una cancha tiene 5.400 m 2 de superficie. |
Medidas de superficie
La unidad de las medidas de superficie es el metro cuadrado (m 2 ), que corresponde a un cuadrado que tiene de lado un metro lineal.
Los múltiplos y submúltiplos del m 2 aumentan y disminuyen de cien en cien y son:
Kilómetro cuadrado (Km 2 )
Hectómetro cuadrado (Hm 2 )
Decámetro cuadrado (Dm 2 )
metro cuadrado (m 2 )
decímetro cuadrado (dm 2 )
centímetro cuadrado (cm 2 )
milímetro cuadrado (mm 2 ).
En el cuadro siguiente mostramos las equivalencias entre ellas:
|
|
Km 2 |
Hm 2 |
Dm 2 |
m 2 |
dm 2 |
cm 2 |
mm 2 |
|
Km 2 |
1 |
100 |
10.000 |
1.000.000 |
100.000.000 |
10.000.000.000 |
1.000.000.000.000 |
|
Hm 2 |
0,01 |
1 |
100 |
10.000 |
1.000.000 |
100.000.000 |
10.000.000.000 |
|
Dm 2 |
0,.0001 |
0,01 |
1 |
100 |
10.000 |
1.000.000 |
100.000.000 |
|
m 2 |
0,000001 |
0,0001 |
0,01 |
1 |
100 |
10.000 |
1.000.000 |
|
dm 2 |
0,00000001 |
0,000001 |
0,0001 |
0,01 |
1 |
100 |
10.000 |
|
cm 2 |
0,0000000001 |
0,00000001 |
0,000001 |
0,0001 |
0,01 |
1 |
100 |
|
mm 2 |
0,000000000001 |
0,0000000001 |
0,00000001 |
0,000001 |
0,0001 |
0,01 |
1 |
Como debe leerse el cuadro:
Por ejemplo:
1 Km 2 es igual a 100 Hm 2
1 Km 2 es igual a 10.000 Dm 2
1 Km 2 es igual a 1.000.000 m 2
1 Km 2 es igual a 100.000.000 dm 2
1 Km 2 es igual a 10.000.000.000 cm 2
1 Km 2 es igual a 1.000.000.000.000 mm 2
Para cada medida es lo mismo.
El cuadro, de aparente complejidad, nos permite hacer fácilmente la conversión entre cualquiera de las medidas.
Veamos un ejemplo:
Fijemos la atención en los cuadros coloreados.
Si nos dan una medida en decímetros cuadrados (dm 2 ) y la multiplicamos por 0,01 tendremos los dm 2 convertidos en metros cuadrados (m 2 ).
En sentido inverso, si nos dan una medida en metros cuadrados (m 2 ) y la dividimos por 0,01 , tendremos los metros cuadrados convertidos en decímetros cuadrados (dm 2 ).
Este juego de multiplicar por los valores de la tabla en sentido horizontal y dividir por los valores en sentido vertical se aplica a cualquiera de las medidas.
Ejercicios:
Convertir 4.000 cm 2 a hectómetros cuadrados (Hm 2 ), a decámetros cuadrados (Dm2) y a milímetros cuadrados (mm 2 )
4.000 • 0,000001 = 0,004 Hm 2
4.000 • 0,0001 = 0,4 Dm 2
4.000 • 10.000 = 40.000.000 mm 2
También podemos hacerlo dividiendo por los valores en sentido vertical:
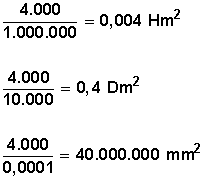
Para no que no se preste a confusión, debemos señalar que, como norma, se aconseja lo siguiente:
Para convertir una magnitud grande a otra más pequeña, se haga una multiplicación.
Para convertir una magnitud pequeña a otra más grande, se haga una división.
Ver: Para resolver problemas de conversión de medidas en el Sistema Métrico Decimal
Medidas de superficie agrarias
Para medir extensiones en el campo se utilizan las llamadas medidas agrarias, que son las siguientes :
La hectárea que equivale al hectómetro cuadrado (Hm 2 ).
1 Ha = 1 Hm 2 = 10 000 m 2
El área equivale al decámetro cuadrado (Dm 2 ).
1 a = 1 Dm 2 = 100 m²
La centiárea equivale al metro cuadrado .
1 ca = 1 m 2
Estas medidas podemos simplificarlas en el cuadro siguiente:
|
|
Ha |
a |
ca |
|
Ha |
1 |
100 |
10.000 |
|
a |
0,01 |
1 |
100 |
|
ca |
0,0001 |
0,01 |
1 |
Hagamos algunos ejercicios:
Expresar en hectáreas:
1) 211.943 a
Según el cuadro superior, podemos multiplicar por 0,01 o dividir por 100 para convertir las hectáreas en áreas.
211.943 : 100 = 2.119,43 ha
2) 356.500 m 2
Sabemos que cada hectárea equivale a 10.000 m 2 , entonces hecemos la división
356.500 : 10.000 = 35,65 ha (35,65 hm 2 )
3) 0,425 km 2
Primero convertimos los Km 2 en m 2 .
0,425 • 1.000.000 = 425.000 m 2
y como sabemos que cada hectárea equivale a 10.000 m 2 , entonces hecemos la división
425.000 : 10.000 = 42.5 ha (42,5 Hm 2 )

|
| Un litro de leche, ocupa un volumen de 1 dm 3 . |
Medidas de volumen
La unidad de las medidas de volumen es el metro cúbico (m 3 ), que es un cubo cuya arista mide un metro lineal..
Los múltiplos y submúltiplos del m 3 aumentan y disminuyen de mil en mil y son:
Kilómetro cúbico (Km 3 )
Hectómetro cúbico (Hm 3 )
Decámetro cúbico (Dm 3 )
metro cúbico (m 3 )
decímetro cúbico (dm 3 )
centímetro cúbico (cm 3 )
milímetro cúbico (mm 3 ).
En el cuadro siguiente mostramos las equivalencias entre ellas:
|
|
Km 3 |
Hm 3 |
Dm 3 |
m 3 |
dm 3 |
cm 3 |
mm 3 |
|
Km 3 |
1 |
1.000 |
1.000.000 |
1.000.000.000 |
1.000.000.000.000 |
1.000.000.000.000.000 |
1.000.000.000.000.000.000 |
|
Hm 3 |
0,001 |
1 |
1.000 |
1.000.000 |
1.000.000.000 |
1.000.000.000.000 |
1.000.000.000.000.000 |
|
Dm 3 |
0,.000001 |
0,001 |
1 |
1.000 |
1.000.000 |
1.000.000.000 |
1.000.000.000.000 |
|
m 3 |
0,000000001 |
0,000001 |
0,001 |
1 |
1.000 |
1.000.000 |
1.000.000.000 |
|
dm 3 |
0,000000000001 |
0,000000001 |
0,000001 |
0,001 |
1 |
1.000 |
1.000.000 |
|
cm 3 |
0,000000000000001 |
0,000000000001 |
0,000000001 |
0,000001 |
0,001 |
1 |
1.000 |
|
mm 3 |
0,000000000000000001 |
0,000000000000001 |
0,000000000001 |
0,000000001 |
0,000001 |
0,001 |
1 |
Como debe leerse el cuadro:
Por ejemplo:
1 Km3 es igual a 1.000 Hm3
1 Km3 es igual a 1.000.000 Dm3
1 Km3 es igual a 1.000.000.000 m3
1 Km3 es igual a 1.000.000.000.000 dm3
1 Km3 es igual a 1.000.000.000.000.000 cm3
1 Km3 es igual a 1.000.000.000.000.000.000 mm3
Para cada medida es lo mismo.
El cuadro, de aparente complejidad, nos permite hacer fácilmente la conversión entre cualquiera de las medidas.
Veamos un ejemplo:
Fijemos la atención en los cuadros coloreados.
Si nos dan una medida en decímetros cúbicos (dm 3 ) y la multiplicamos por 0,001 tendremos los dm 3 convertidos en metros cúbicos (m 3 ).
En sentido inverso, si nos dan una medida en metros cúbicos (m 3 ) y la dividimos por 0,001 , tendremos los metros cúbicos convertidos en decímetros cúbicos (dm 3 ).
Este juego de multiplicar por los valores de la tabla en sentido horizontal y dividir por los valores en sentido vertical se aplica a cualquiera de las medidas.
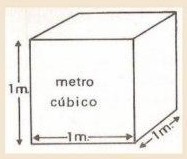
|
| 1 m 3 es igual a 1.000 dm 3 |
Ejercicios:
Convertir 4.000 cm 3 a hectómetros cúbicos (Hm 3 ), a decámetros cúbicos (Dm 3 ) y a milímetros cúbicos (mm 3 )
4.000 • 0,000000001 = 0,000004 Hm 3
4.000 • 0,000001 = 0,004 Dm 3
4.000 • 1.000.000 = 4.000.000.000 mm 3
También podemos hacerlo dividiendo por los valores en sentido vertical:
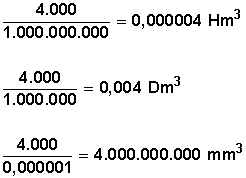
Para no que no se preste a confusión, debemos señalar que, como norma, se aconseja lo siguiente:
Para convertir una magnitud grande a otra más pequeña, se haga una multiplicación.
Para convertir una magnitud pequeña a otra más grande, se haga una división.
Ver: Para resolver problemas de conversión de medidas en el Sistema Métrico Decimal
Relación entre unidades de capacidad, volumen y masa
Existe una relación muy directa entre el volumen y capacidad. 1 l (un litro) es la capacidad que contiene un recipiente cúbico de 1 dm de arista; es decir, la capacidad contenida en un volumen de 1 dm 3 .
También existe una relación entre el volumen y la masa de agua. 1 g (un gramo) equivale a 1 cm 3 de agua pura a 4° C .
| Capacidad |
Volumen |
Masa (de agua) |
|
1 Kl |
1 m 3 |
1 t |
|
1 l |
1 dm 3 |
1 Kg |
|
1 ml |
1 cm 3 |
1 g |
Ejemplos
Expresar en litros:
1) 23,2 m 3
Según el cuadro, 1 l es igual a 1 dm 3 , por eso convertimos los m 3 a dm 3
23,2 m 3 • 1.000 = 23.200 dm 3 = 23.200 l
2) 0,07 m 3 = 70 dm 3 = 70 l
3) 5.2 dm 3 = 5.2 l
4) 8 800 cm 3 = = 8.8 dm 3 = 8.8 l
Unidades de tiempo
Las unidades de tiempo no pertenecen al Sistema Métrico Decimal , ya que están relacionadas entre sí por múltiplos o submúltiplos de 60. El tiempo es una magnitud del Sistema Sexagesimal . Pero el segundo (s) , como unidad de tiempo, se incluye en el Sistema Internacional de Unidades .
Ir a: Metrología
Fuentes Internet:
http://www.vitutor.com/di/m/a_1.html
http://www.sectormatematica.cl/contenidos/sismetdec.htm
http://www.vitutor.com/di/m/a_6.html
http://www.vitutor.com/di/m/a_7.html
http://www.vitutor.com/di/m/a_10.html

