Plano inclinado 02 |
Plano inclinado y ángulo
Veíamos en el apartado anterior (Plano inclinado 01) que la idea central de usar el plano inclinado es disminuir la fuerza necesaria para trasladar objetos (que pesan) hacia arriba.
Recordemos también lo dicho sobre identificar las fuerzas que actúan en el plano inclinado:
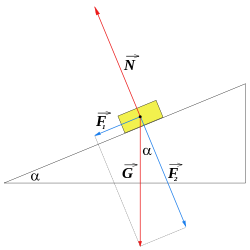
|
| Ilustración de las fuerzas que actúan sobre un sólido puesto en un Plano inclinado. |
En la figura de arriba vemos una línea roja vertical, dirigida hacia la tierra y formando ángulo recto con ella, identificada como G. Esta representa el peso que posee el objeto y que depende de su masa y de la fuerza de gravedad.
Esta fuerza G, o peso del objeto, puesto en el plano inclinado, se descompone en dos fuerzas, F 1 y F 2 , representadas en el gráfico en color azul.
F 1 es una fuerza paralela al plano inclinado y es la fuerza a vencer para mover el objeto hacia arriba.
F 2 es perpendicular al plano inclinado y se denomina fuerza normal . También conocida como la fuerza de reacción ejercida sobre el cuerpo por el plano como consecuencia de la tercera ley de Newton .
También se agrega la fuerza de rozamiento (de roce o de fricción) que pone resistencia al desplazamiento del objeto debido al tipo de superficie del plano inclinado. (Por el momento, haremos abstracción de esta fuerza para nuestros ejercicios.)
Conocer el valor de la fuerza paralela (F 1 )
Repetimos lo dicho antes: La idea central de usar el plano inclinado es disminuir la fuerza necesaria para trasladar objetos (que pesan) hacia arriba.
Ahora, el sistema o fórmula para encontrar ese valor (de la fuerza menor a la que indica su peso) depende de los datos que se nos proporcionen al enfrentarnos a un ejercicio.
En el apartado anterior vimos cómo calcular la fuerza paralela si conocemos la longitud del plano, el peso-fuerza del objeto y la altura a la cual llegar.
Ahora veremos:
Cálculo de la fuerza conociendo solo el ángulo y el peso-fuerza
En este apartado, veremos cómo calcular esa fuerza si los datos que nos dan son solo el peso (en kilopondios o kilogramos-fuerza) y el ángulo agudo que forma el plano inclinado con la superficie de la tierra.
Volvamos al dibujo ilustrativo que mostramos arriba:

Ahora nos fijamos que, junto a las fuerzas descritas, está marcado el ángulo alfa (α) formado por el plano inclinado con el suelo horizontal.
La tarea consiste en averiguar el valor de la fuerza F 1 (fuerza paralela) si conocemos el ángulo del plano con el suelo y el valor de la fuerza original (o peso en kilopondios) de un objeto puesto sobre un plano inclinado. (Esto, sin tener en cuenta el rozamiento o fuerza de roce).
En algunos ejercicios, G se identifica con P y F 1 y F 2 se identifican como P x y P y .
Ver: Fuerza de roce o rozamiento .
Veamos cómo se opera revisando el siguiente ejemplo:
Colocamos un peso de 200 kilopondios (kilogramos-fuerza) en una rampa, que forma un ángulo de 30° con el suelo. Suponemos que no se desliza, no resbala:
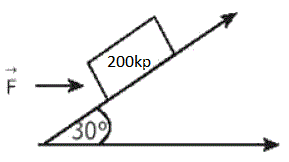
Tenemos que calcular la fuerza que debemos vencer para subir el peso (P) de 200 kilopondios.
Veamos lo que sucede con ese peso (o cualquier otro) colocado en un plano cuya inclinación sea α (en nuestro ejemplo vale 30°):
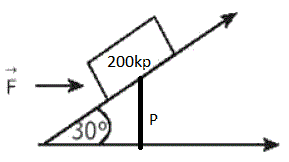
El peso situado en el plano ejerce una fuerza-peso P (200 kp) que es perpendicular respecto del suelo.
A la fuerza-peso (P) la consideramos como la resultante de otras dos: P x y P y :
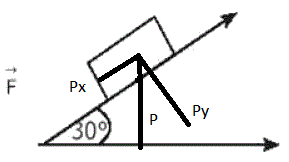
Entonces:
En un plano inclinado que forma un ángulo de 30° con la horizontal del suelo tenemos un peso de 200 kilos-fuerza.
Nos preguntamos: ¿Cuánto vale la fuerza paralela al plano (P x ) y cuánto la fuerza perpendicular (fuerza normal) al mismo (P y )?
Solución:
Para conocer la fuerza paralela (P x ) usaremos la fórmula
P x = P • sen α
Ver: Teorema del seno
Para conocer la fuerza perpendicular (P y ) (llamada también Normal) usaremos
P y = P • cos α
Ver: Teorema del coseno
Sustituimos los valores y hacemos las operaciones:
P x = P • sen α → 200 • sen 30° = 200 • 0,5 = 100 kilos-fuerza, que expresados en Newtons:
100 • 9,8 = 980 N
P y = P • cos α → 200 • cos 30° = 200 • 0,866 = 173 kilos-fuerza, que expresados en Newtons:
173 • 9,8 = 1.695 N
Nota:
Como sabemos que P = m • g (El peso expresado en Newtons), las fórmulas se pueden usar como
P x = m • g • sen α → 200 • 9,8 • sen 30° = 200 • 9,8 • 0,5 = 980 N
P y = m • g • cos α → 200 • cos 30° = 200 • 0,866 = 1.695 N
Nota:
Recuerden que los valores de seno y coseno deben ser entregados por el docente o, en su defecto, deben obtenerse con una calculadora.
Volver a: Plano inclinado 01
Fuentes Internet:
Video explicativo en
Además:
https://www.youtube.com/watch?v=DgOq1XEIErM
https://www.youtube.com/watch?v=iCAadj5DM8U
http://asimov.com.ar/wp-content/uploads/6-Plano-Inclinado-10-Pag-.pdf
https://es.wikihow.com/hallar-la-fuerza-normal

