Número áureo o número de oro

El número áureo es un número algebraico  irracional (decimal sin periodo), representado por la letra griega φ (phi) (en minúscula) o Φ (Phi) (en mayúscula) en honor al escultor griego Fidias . Su valor matemático es 1,618 aproximadamente ya que sus decimales son infinitos y en rigor representa una proporción entre dos valores .

También se lo ha llamado número de oro, razón extrema y media, razón áurea, razón dorada, media áurea, proporción áurea, sección divina, sección de oro, proporción divina, proporción dorada, canon áureo  y regla de oro , pero el origen exacto del término número áureo, en cualquiera de sus nombres, es bastante incierto, aunque generalmente se sitúa en Alemania, durante la primera mitad del siglo XIX.

Lo cierto es que esta proporción áurea posee muchas propiedades interesantes y fue descubierta en la antigüedad, no como una expresión aritmética, sino como relación o proporción entre dos segmentos de una recta; es decir, una construcción geométrica.

Se encuentra tanto en algunas figuras geométricas como en la naturaleza: en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, etcétera.

Muchos han sido los artistas, humanistas y matemáticos se han ocupado de él, a tal punto que la proporción que representa este número áureo ha desempeñado un importante papel en los intentos de encontrar una explicación matemática a la belleza, de reducir ésta a un número, de encontrar “la cifra ideal ".

Es por esto que se atribuye un carácter estético a los objetos cuyas medidas guardan la proporción áurea. Algunos incluso creen que posee una importancia mística. En el transcurso de la historia, se ha atribuido su inclusión en el diseño de diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido cuestionados por los estudiosos de las matemáticas y el arte.

Ver: El número de oro en el arte, el diseño y la naturaleza

Proporción áurea

Para aterrizar el concepto, o “visualizarlo”, diremos que el número áureo es el valor numérico de la proporción que guardan entre sí dos segmentos de recta a y b (a más largo que b ), que cumplen la siguiente relación:

La longitud total, o suma de los dos segmentos (a + b) , es al segmento mayor (a) , lo que este segmento a es al segmento menor (b) .

Escrito como ecuación algebraica :

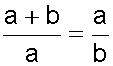
Lo cual significa que dos segmentos (a y b) están en proporción áurea si se cumple que, al dividir la longitud total (a + b) entre la del segmento mayor (a), obtengamos el mismo resultado que al dividir la longitud del segmento mayor (a) entre la longitud del menor (b).

De acuerdo con el rectángulo áureo de Euclides (que luego veremos), podemos llegar a la solución positiva de una ecuación de segundo grado , que nos lleva finalmente a

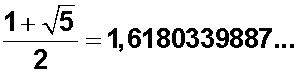
lo cual nos da el valor del número áureo, equivalente a la relación

Ver: Raíz cuadrada de cinco

Construcción geométrica del número áureo

Aceptada la ecuación matemática que nos permite conocer valores que están en proporción áurea, veamos ahora cómo podemos lograr la construcción geométrica de esta proporción de oro .

Básicamente, hay dos formas de calcular u obtener geométricamente la sección áurea:

1) En la primera forma se nos plantea la división de un segmento (AB) en media y extrema razón.

Si tenemos (o conocemos) un solo segmento (AB en la figura arriba), existe tan solo un punto F que haga posible esta relación entre los segmentos obtenidos y que verifique la proporción áurea.

Construcción geométrica:

Como vemos en la siguiente figura,

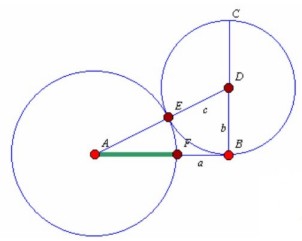
primero, levantamos la perpendicular BD con una altura igual a AB/2 (la mitad del segmento conocido AB); hacemos circunferencia con centro en D y radio BD y unimos D con A que es la hipotenusa del triángulo ABD y obtenemos E; ahora con centro en A y radio AE calculamos el punto F..

2) En la segunda forma, debemos hallar un segmento FB (desconocido), que esté en relación áurea con otro segmento dado AF.

Para calcularlo, construimos un cuadrado de lados AF, y con centro en AF/2 (E) y radio ED, trazamos un arco hasta cortar la prolongación de AF y obtenemos el segmento que buscábamos, como vemos en la figura siguente:

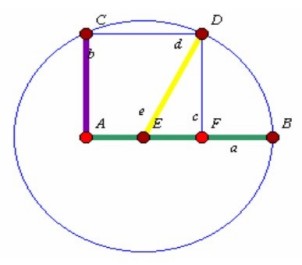
Ver: El triángulo áureo de Euclides

Fuentes Internet:

https://es.wikipedia.org/wiki/N%C3%BAmero_%C3%A1ureo

http://matematicas.uclm.es/ita-cr/web_matematicas/trabajos/240/La_seccion_aurea_en%20arte.pdf

Revisar la página

http://www.dzoom.org.es/descubre-que-es-la-proporcion-aurea-y-como-puede-ayudarte-en-la-composicion-de-tus-fotos/
sobre la composición fotográfica y el número áureo.

Ver, además,

http://laproporcionperfecta.blogspot.cl/2011/06/numero-de-oro.html