Sistemas de fuerzas

Fuerzas aplicadas sobre sólidos

El efecto más visible de las fuerzas es producir deformaciones en los cuerpos, pero hay cuerpos que no se deforman; por eso diferenciamos dos tipos de sólidos: deformables e indeformables o rígidos .

Sólidos deformables

Sólido rígido

Sometidos a una fuerza, los sólidos rígidos pueden realizar dos tipos de movimiento: de traslación o de rotación , según el punto donde se aplique la fuerza.

Sistemas de fuerzas.

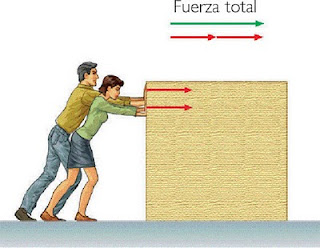
Por lo general, varias fuerzas actúan sobre un cuerpo.

Con frecuencia varias fuerzas actúan al mismo tiempo sobre un mismo cuerpo.

Cuando existe más de una fuerza tenemos lo que se denomina un Sistema de Fuerzas .

Cada una de las fuerzas actuantes recibe el nombre de componente del sistema.

Cuando varias fuerzas actúan sobre un mismo cuerpo, siempre es posible sustituirlas por una única fuerza capaz de producir el mismo efecto.

Esa única fuerza que reemplaza a todas se denomina fuerza Resultante o simplemente Resultante.

Se llama fuerza equilibrante la fuerza igual y contraria a la resultante.

La resultante de un sistema de fuerzas se puede representar en forma gráfica, pero también es posible calcular analíticamente (en forma matemática) su valor o módulo.

Representación gráfica de una fuerza Resultante

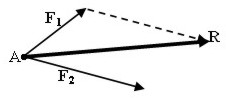
En la figura, las fuerzas F1 y F2 forman un sistema de fuerzas. Son las componentes del sistema.

La línea punteada es la representación de F2.

La diagonal desde A hasta el final de dicha línea punteada corresponde a la fuerza resultante (R) del sistema.

Para mostrar gráficamente la resultante de un sistema de fuerzas se procede de la siguiente manera:

1) A partir del extremo de la primera fuerza, se representa (se copia o se dibuja) la segunda fuerza con su intensidad, dirección y sentido.

2) El vector que une el origen de la primera fuerza con el final de la segunda fuerza representa, en intensidad, dirección y sentido, la resultante del sistema.

Diferentes sistemas de fuerzas

Básicamente existen 3 sistemas:

Sistemas de Fuerzas Colineales

Las fuerzas están sobre la misma dirección. En este caso, tenemos dos situaciones:

Sistema de fuerzas que actúan en el mismo sentido.

Sistema de fuerzas que actúan en sentido contrario.

Sistemas de Fuerzas Paralelas

Aplicación práctica de fuerzas concurrentes angulares.

Como su nombre lo indica, son paralelas y existen métodos para calcular su Resultante.

Pero si van al mismo sentido la Resultante sera la suma de ambas. Si van en sentido contrario será la resta entre ellas. Sin embargo lo que lleva más trabajo es encontrar el punto de aplicación.

Entonces, dependiendo del sentido, tenemos:

Sistema de fuerzas paralelas y en el mismo sentido.

Sistema de fuerzas paralelas de sentido contrario.

Par de fuerzas .

Sistema de Fuerzas Concurrentes angulares

Son aquellos sistemas en los cuales hay fuerzas con direcciones distintas pero que se cruzan en un punto determinado, ya sean sus vectores o sus prolongaciones.

Para hallar analíticamente (en forma matemática) la resultante hay que trabajar con las fórmulas de seno, coseno, tangente y el Teorema de Pitágoras .

Respecto a este tipo de fuerzas, veremos los tópicos:

Sistema de fuerzas angulares.

Torque o Momento de una fuerza.

Descomposición de fuerzas .