Isometría y transformaciones isométricas |
La palabra isometría proviene del griego iso (prefijo que significa igual o mismo ) y metria (que significa medir ). Por ello, una definición adecuada para isometría sería igual medida .
|
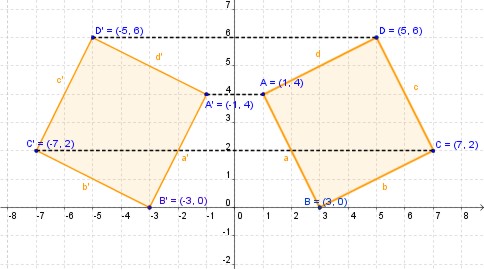
| Cuadrado simétrico, una construcción isométrica. |
Se denomina transformación isométrica de una figura en el plano aquella transformación que no altera ni la forma ni el tamaño de la figura en cuestión y que solo involucra un cambio de posición de ella (en la orientación o en el sentido), resultando que la figura inicial y la final son semejantes , y geométricamente congruentes .
Además de relacionarse con la semejanza y la congruencia en las figuras planas, las transformaciones isométricas tienen una estrecha relación con la expresión artística, apoyada en la construcción geométrica (por ejemplo, en las teselaciones ).
Por ello, en el aula, el tópico isometría se puede desarrollar en torno a dos aspectos temáticos:
1.- Actividades en torno a la posibilidad de embaldosar superficies planas con figuras geométricas ( teselaciones ).
2.- Actividades asociadas al diseño, descripción y reconocimiento de transformaciones isométricas
Respecto a la isometría y a las posibilidades de transformaciones de figuras, se pueden describir tres tipos de ejecución: por traslación , por rotación y por simetría (o reflexión ).
Cualquiera que sea el método aplicado para realizar una transformación isométrica en un plano es imprescindible trabajar sobre un sistema de coordenadas .
Sistema de coordenadas
Un sistema de coordenadas bidimensional (en un plano) es un sistema en el cual un punto puede moverse en todas direcciones, manteniéndose siempre en el mismo plano.
El sistema más usado es el sistema de coordenadas rectangular u ortogonal, más conocido como Plano Cartesiano .
Este sistema está formado por dos rectas perpendiculares entre sí llamadas ejes de coordenadas ( eje de las x y eje de las y ).
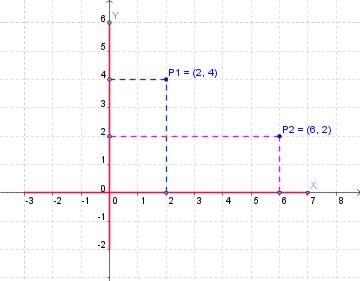
Las coordenadas de un punto determinan dicho punto. Conocidas las coordenadas de ese punto, puede ser localizado en el plano, como en la figura de abajo donde se han localizado los puntos P1 y P2 .
|
| Coordenadas para los puntos P1 y P2. |
Transformaciones isométricas por Traslación
En una transformación isométrica por traslación se realiza un cambio de posición de la figura en el plano. Es un cambio de lugar, determinado por un vector .
|
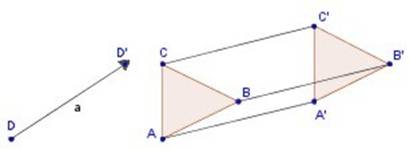
| Traslación del punto D a su imagen D’ (vector a = DD’) y traslación de un triángulo. |
En general, se llama traslación de vector (v) a la isometría que a cada punto m del plano le hace corresponder un punto m' del mismo plano, tal que mm' es igual a v .
Las traslaciones isométricas están marcadas por tres elementos:
La dirección, si es horizontal, vertical un oblicua.
El sentido, derecha, izquierda, arriba y abajo.
Y la magnitud del desplazamiento que se refiere a cuánto se desplazó la figura en una unidad de medida.
Ver: PSU: Geometría, Pregunta 04_2006
Transformaciones isométricas por Rotación
|
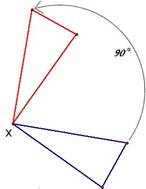
| Rotación del triángulo, respecto del punto X. |
Una rotación , en geometría, es un movimiento de cambio en la orientación de un cuerpo; de forma que, dado un punto cualquiera del mismo, este permanece a una distancia constante de un punto fijo, y tiene las siguientes características:
Un punto denominado centro de rotación.
Un ángulo
Un sentido de rotación.
Estas transformaciones por rotación pueden ser positivas o negativas dependiendo del sentido de giro.
Para el primer caso debe ser un giro en sentido contrario a las manecillas del reloj, y será negativo el giro cuando sea en sentido de las manecillas.
Transformaciones isométricas por Simetría
El concepto se simetría se nos presenta de forma natural y nos entrega ejemplos de gran belleza en nuestro entorno.


|
|
|
| Simetría en la naturaleza. |
Tanto la figura del escarabajo como de la mariposa se ven simétricas, pues si trazamos una línea recta en el centro de cada una, la parte que está a la derecha de la línea sería exactamente igual a la parte que está a la izquierda de esa misma línea.
Sobre la base de estos dos ejemplos, se descubre fácilmente que hay una transformación que hace que la parte izquierda de la figura sea un reflejo de la parte derecha sin cambiar su forma ni sus dimensiones.
Esto nos lleva a afirmar que Simetría es la correspondencia exacta (un reflejo) en la disposición regular de las partes o puntos de un cuerpo o figura con relación a un punto (centro), una recta ( eje de simetría ) o un plano.
Definido o conocido el concepto de simetría , podemos agregar que la simetría puede ser central o axial
Ver: PSU: Geometría; Pregunta 03_2006
Simetría central
La simetría central , en geometría, es una transformación en la que a cada punto se le asocia otro punto, que debe cumplir las siguientes condiciones:
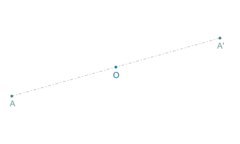
a) El punto y su imagen estén a igual distancia de un punto llamado centro de simetría .
b) El punto, su imagen y el centro de simetría pertenezcan a una misma recta.
|
| Simetría central del punto A. |
|
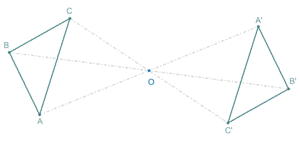
| Simetría central del triángulo ABC, respecto del punto O. |
Según estas definiciones, con una simetría central se obtiene la misma figura con una rotación de 180 grados.
Simetría axial
La simetría axial , en geometría, es una transformación respecto de un eje de simetría , en la cual, a cada punto de una figura se asocia otro punto llamado imagen, que cumple con las siguientes condiciones:
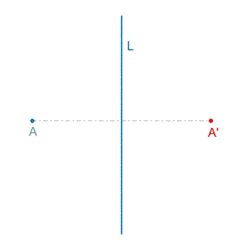
a) La distancia de un punto y su imagen al eje de simetría, es la misma.
b) El segmento que une un punto con su imagen, es perpendicular al eje de simetría.
|
| Simetría axial del punto A. |
|
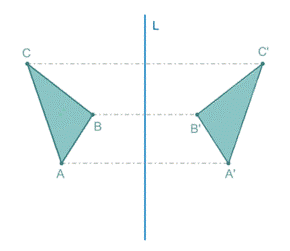
| Simetría axial de un triángulo. |
En la simetría axial se conservan las distancias pero no el sentido de los ángulos. El eje de simetría es la mediatriz del segmento AA'.
Ver: PSU: Geometría; Pregunta 04_2005

|
| La imagen de un objeto reflejada en un espejo plano, es un ejemplo de transformación isométrica: la simetría. |
Para ver un ejercicio sobre
Dilatación y tralación de una figura geométrica
Fuentes Internet:
fisica.usach.cl/~cecilia/word/geo2006clase8.doc
http://isometricastransformaciones.blogspot.com/
http://es.wikipedia.org/wiki/Isometr%C3%ADa_af%C3%ADn
Ver en Youtube
http://www.youtube.com/watch?v=Q3Feur2f9qY



